Complex Numbers, Mean, and Classification

• Complex numbers

  • Absolute value

• Evenly spaced numbers

• Mean

  • Arithmetic mean

  • Geometric mean

  • Harmonic mean

• Classification

Complex Numbers

A complex number \(z\) is represented by \(z = x + j* y\), where \(x\) and \(y\) are real numbers.

c1 = complex(0, 0)

print(c1)

0j

x = 2
y = 3
c2 = complex(x, y)

print(c2)

(2+3j)

Absolute value

Absolute value of a complex number \(z = x + j* y\) is obtained by the formula \(\sqrt {(x^2 + y^2)}\)

from math import sqrt

absc2 = sqrt(x**2 + y**2)
print(absc2)

3.605551275463989

Another way is to use the function \(abs()\).

absc2 = abs(c2)
print(absc2)

3.605551275463989

absc1 = abs(c1)
print(absc1)

0.0

Evenly spaced numbers

import numpy as np

np.linspace(1.0, 5.0, num=5)

array([1., 2., 3., 4., 5.])

import numpy as np

np.linspace(1.0, 5.0, num=10)

array([1.        , 1.44444444, 1.88888889, 2.33333333, 2.77777778,
       3.22222222, 3.66666667, 4.11111111, 4.55555556, 5.        ])

Mean

Arithmetic mean

If \(a_1, a_2, \ldots, a_n\) are numbers, then the arithmetic mean is obtained by:

\[A=\frac{1}{n}\sum_{i=1}^n a_i=\frac{a_1+a_2+\cdots+a_n}{n}\]

num = np.linspace(1.0, 100.0, num=100)

a = np.mean(num)
print(a)

50.5

Geometric Mean

If \(a_1, a_2, \ldots, a_n\) are numbers, then the arithmetic mean is obtained by:

\[\left(\prod_{i=1}^n a_i\right)^\frac{1}{n} = \sqrt[n]{a_1 a_2 \cdots a_n}\]

from scipy.stats import gmean

g = gmean(num)
print(g)

37.992689344834304

Harmonic Mean

If \(a_1, a_2, \ldots, a_n\) are numbers, then the harmonic mean is obtained by:

\[H = \frac{n}{\frac1{a_1} + \frac1{a_2} + \cdots + \frac1{a_n}} = \frac{n}{\sum\limits_{i=1}^n \frac1{a_i}} = \left(\frac{\sum\limits_{i=1}^n a_i^{-1}}{n}\right)^{-1}.\]

from scipy.stats import hmean

h = hmean(num)
print(h)

19.277563597396004

Classification

Understanding IRIS dataset

from sklearn.datasets import load_iris

data = load_iris()

# Target Classes and Names
for target, name in enumerate(data.target_names):
    print(target, name)

0 setosa
1 versicolor
2 virginica

# Features
for feature in data.feature_names:
    print(feature)

sepal length (cm)
sepal width (cm)
petal length (cm)
petal width (cm)

X = data.data
Y = data.target

print(f"Data size: {len(X)}")

Data size: 150

# Printing the data

for x, y in zip(X, Y):
    print(f" {x}: {y} ({data.target_names[y]})")

 [5.1 3.5 1.4 0.2]: 0 (setosa)
 [4.9 3.  1.4 0.2]: 0 (setosa)
 [4.7 3.2 1.3 0.2]: 0 (setosa)
 [4.6 3.1 1.5 0.2]: 0 (setosa)
 [5.  3.6 1.4 0.2]: 0 (setosa)
 [5.4 3.9 1.7 0.4]: 0 (setosa)
 [4.6 3.4 1.4 0.3]: 0 (setosa)
 [5.  3.4 1.5 0.2]: 0 (setosa)
 [4.4 2.9 1.4 0.2]: 0 (setosa)
 [4.9 3.1 1.5 0.1]: 0 (setosa)
 [5.4 3.7 1.5 0.2]: 0 (setosa)
 [4.8 3.4 1.6 0.2]: 0 (setosa)
 [4.8 3.  1.4 0.1]: 0 (setosa)
 [4.3 3.  1.1 0.1]: 0 (setosa)
 [5.8 4.  1.2 0.2]: 0 (setosa)
 [5.7 4.4 1.5 0.4]: 0 (setosa)
 [5.4 3.9 1.3 0.4]: 0 (setosa)
 [5.1 3.5 1.4 0.3]: 0 (setosa)
 [5.7 3.8 1.7 0.3]: 0 (setosa)
 [5.1 3.8 1.5 0.3]: 0 (setosa)
 [5.4 3.4 1.7 0.2]: 0 (setosa)
 [5.1 3.7 1.5 0.4]: 0 (setosa)
 [4.6 3.6 1.  0.2]: 0 (setosa)
 [5.1 3.3 1.7 0.5]: 0 (setosa)
 [4.8 3.4 1.9 0.2]: 0 (setosa)
 [5.  3.  1.6 0.2]: 0 (setosa)
 [5.  3.4 1.6 0.4]: 0 (setosa)
 [5.2 3.5 1.5 0.2]: 0 (setosa)
 [5.2 3.4 1.4 0.2]: 0 (setosa)
 [4.7 3.2 1.6 0.2]: 0 (setosa)
 [4.8 3.1 1.6 0.2]: 0 (setosa)
 [5.4 3.4 1.5 0.4]: 0 (setosa)
 [5.2 4.1 1.5 0.1]: 0 (setosa)
 [5.5 4.2 1.4 0.2]: 0 (setosa)
 [4.9 3.1 1.5 0.2]: 0 (setosa)
 [5.  3.2 1.2 0.2]: 0 (setosa)
 [5.5 3.5 1.3 0.2]: 0 (setosa)
 [4.9 3.6 1.4 0.1]: 0 (setosa)
 [4.4 3.  1.3 0.2]: 0 (setosa)
 [5.1 3.4 1.5 0.2]: 0 (setosa)
 [5.  3.5 1.3 0.3]: 0 (setosa)
 [4.5 2.3 1.3 0.3]: 0 (setosa)
 [4.4 3.2 1.3 0.2]: 0 (setosa)
 [5.  3.5 1.6 0.6]: 0 (setosa)
 [5.1 3.8 1.9 0.4]: 0 (setosa)
 [4.8 3.  1.4 0.3]: 0 (setosa)
 [5.1 3.8 1.6 0.2]: 0 (setosa)
 [4.6 3.2 1.4 0.2]: 0 (setosa)
 [5.3 3.7 1.5 0.2]: 0 (setosa)
 [5.  3.3 1.4 0.2]: 0 (setosa)
 [7.  3.2 4.7 1.4]: 1 (versicolor)
 [6.4 3.2 4.5 1.5]: 1 (versicolor)
 [6.9 3.1 4.9 1.5]: 1 (versicolor)
 [5.5 2.3 4.  1.3]: 1 (versicolor)
 [6.5 2.8 4.6 1.5]: 1 (versicolor)
 [5.7 2.8 4.5 1.3]: 1 (versicolor)
 [6.3 3.3 4.7 1.6]: 1 (versicolor)
 [4.9 2.4 3.3 1. ]: 1 (versicolor)
 [6.6 2.9 4.6 1.3]: 1 (versicolor)
 [5.2 2.7 3.9 1.4]: 1 (versicolor)
 [5.  2.  3.5 1. ]: 1 (versicolor)
 [5.9 3.  4.2 1.5]: 1 (versicolor)
 [6.  2.2 4.  1. ]: 1 (versicolor)
 [6.1 2.9 4.7 1.4]: 1 (versicolor)
 [5.6 2.9 3.6 1.3]: 1 (versicolor)
 [6.7 3.1 4.4 1.4]: 1 (versicolor)
 [5.6 3.  4.5 1.5]: 1 (versicolor)
 [5.8 2.7 4.1 1. ]: 1 (versicolor)
 [6.2 2.2 4.5 1.5]: 1 (versicolor)
 [5.6 2.5 3.9 1.1]: 1 (versicolor)
 [5.9 3.2 4.8 1.8]: 1 (versicolor)
 [6.1 2.8 4.  1.3]: 1 (versicolor)
 [6.3 2.5 4.9 1.5]: 1 (versicolor)
 [6.1 2.8 4.7 1.2]: 1 (versicolor)
 [6.4 2.9 4.3 1.3]: 1 (versicolor)
 [6.6 3.  4.4 1.4]: 1 (versicolor)
 [6.8 2.8 4.8 1.4]: 1 (versicolor)
 [6.7 3.  5.  1.7]: 1 (versicolor)
 [6.  2.9 4.5 1.5]: 1 (versicolor)
 [5.7 2.6 3.5 1. ]: 1 (versicolor)
 [5.5 2.4 3.8 1.1]: 1 (versicolor)
 [5.5 2.4 3.7 1. ]: 1 (versicolor)
 [5.8 2.7 3.9 1.2]: 1 (versicolor)
 [6.  2.7 5.1 1.6]: 1 (versicolor)
 [5.4 3.  4.5 1.5]: 1 (versicolor)
 [6.  3.4 4.5 1.6]: 1 (versicolor)
 [6.7 3.1 4.7 1.5]: 1 (versicolor)
 [6.3 2.3 4.4 1.3]: 1 (versicolor)
 [5.6 3.  4.1 1.3]: 1 (versicolor)
 [5.5 2.5 4.  1.3]: 1 (versicolor)
 [5.5 2.6 4.4 1.2]: 1 (versicolor)
 [6.1 3.  4.6 1.4]: 1 (versicolor)
 [5.8 2.6 4.  1.2]: 1 (versicolor)
 [5.  2.3 3.3 1. ]: 1 (versicolor)
 [5.6 2.7 4.2 1.3]: 1 (versicolor)
 [5.7 3.  4.2 1.2]: 1 (versicolor)
 [5.7 2.9 4.2 1.3]: 1 (versicolor)
 [6.2 2.9 4.3 1.3]: 1 (versicolor)
 [5.1 2.5 3.  1.1]: 1 (versicolor)
 [5.7 2.8 4.1 1.3]: 1 (versicolor)
 [6.3 3.3 6.  2.5]: 2 (virginica)
 [5.8 2.7 5.1 1.9]: 2 (virginica)
 [7.1 3.  5.9 2.1]: 2 (virginica)
 [6.3 2.9 5.6 1.8]: 2 (virginica)
 [6.5 3.  5.8 2.2]: 2 (virginica)
 [7.6 3.  6.6 2.1]: 2 (virginica)
 [4.9 2.5 4.5 1.7]: 2 (virginica)
 [7.3 2.9 6.3 1.8]: 2 (virginica)
 [6.7 2.5 5.8 1.8]: 2 (virginica)
 [7.2 3.6 6.1 2.5]: 2 (virginica)
 [6.5 3.2 5.1 2. ]: 2 (virginica)
 [6.4 2.7 5.3 1.9]: 2 (virginica)
 [6.8 3.  5.5 2.1]: 2 (virginica)
 [5.7 2.5 5.  2. ]: 2 (virginica)
 [5.8 2.8 5.1 2.4]: 2 (virginica)
 [6.4 3.2 5.3 2.3]: 2 (virginica)
 [6.5 3.  5.5 1.8]: 2 (virginica)
 [7.7 3.8 6.7 2.2]: 2 (virginica)
 [7.7 2.6 6.9 2.3]: 2 (virginica)
 [6.  2.2 5.  1.5]: 2 (virginica)
 [6.9 3.2 5.7 2.3]: 2 (virginica)
 [5.6 2.8 4.9 2. ]: 2 (virginica)
 [7.7 2.8 6.7 2. ]: 2 (virginica)
 [6.3 2.7 4.9 1.8]: 2 (virginica)
 [6.7 3.3 5.7 2.1]: 2 (virginica)
 [7.2 3.2 6.  1.8]: 2 (virginica)
 [6.2 2.8 4.8 1.8]: 2 (virginica)
 [6.1 3.  4.9 1.8]: 2 (virginica)
 [6.4 2.8 5.6 2.1]: 2 (virginica)
 [7.2 3.  5.8 1.6]: 2 (virginica)
 [7.4 2.8 6.1 1.9]: 2 (virginica)
 [7.9 3.8 6.4 2. ]: 2 (virginica)
 [6.4 2.8 5.6 2.2]: 2 (virginica)
 [6.3 2.8 5.1 1.5]: 2 (virginica)
 [6.1 2.6 5.6 1.4]: 2 (virginica)
 [7.7 3.  6.1 2.3]: 2 (virginica)
 [6.3 3.4 5.6 2.4]: 2 (virginica)
 [6.4 3.1 5.5 1.8]: 2 (virginica)
 [6.  3.  4.8 1.8]: 2 (virginica)
 [6.9 3.1 5.4 2.1]: 2 (virginica)
 [6.7 3.1 5.6 2.4]: 2 (virginica)
 [6.9 3.1 5.1 2.3]: 2 (virginica)
 [5.8 2.7 5.1 1.9]: 2 (virginica)
 [6.8 3.2 5.9 2.3]: 2 (virginica)
 [6.7 3.3 5.7 2.5]: 2 (virginica)
 [6.7 3.  5.2 2.3]: 2 (virginica)
 [6.3 2.5 5.  1.9]: 2 (virginica)
 [6.5 3.  5.2 2. ]: 2 (virginica)
 [6.2 3.4 5.4 2.3]: 2 (virginica)
 [5.9 3.  5.1 1.8]: 2 (virginica)

from sklearn.model_selection import train_test_split

# Random state ensures reproducibility
X_train, X_test, Y_train, Y_test = train_test_split(
    X, Y, test_size=0.33, random_state=42
)

print(f"Training data size: {len(X_train)}")
print(f"Test data size: {len(X_test)}")

Training data size: 100
Test data size: 50

from sklearn.metrics import ConfusionMatrixDisplay
import matplotlib.pyplot as plot


def display_confusion_matrix(classifier, title):
    disp = ConfusionMatrixDisplay.from_estimator(
        classifier,
        X_test,
        Y_test,
        display_labels=data.target_names,
        cmap=plot.cm.Blues,
        normalize="true",
    )
    disp.ax_.set_title(title)
    plot.show()

## Classifier
from sklearn import svm, metrics

for kernel in ["linear", "rbf", "poly"]:
    print("")
    classifier = svm.SVC(kernel=kernel, gamma=10)
    classifier.fit(X_train, Y_train)

    predicted_values = classifier.predict(X_test.reshape((X_test.shape[0], -1)))

    # classification report
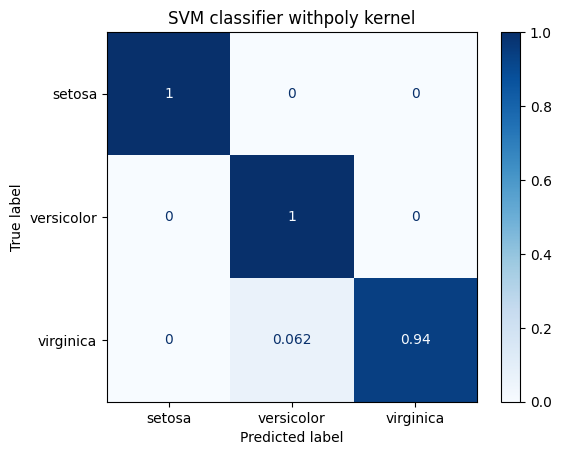
    title = "SVM classifier with" + kernel + " kernel"
    print(metrics.classification_report(Y_test, predicted_values))
    display_confusion_matrix(classifier, title)

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        19
           1       1.00      1.00      1.00        15
           2       1.00      1.00      1.00        16

    accuracy                           1.00        50
   macro avg       1.00      1.00      1.00        50
weighted avg       1.00      1.00      1.00        50

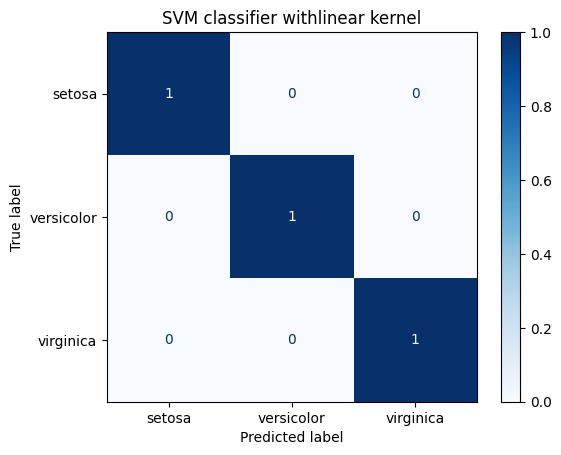
              precision    recall  f1-score   support

           0       1.00      0.95      0.97        19
           1       0.94      1.00      0.97        15
           2       0.94      0.94      0.94        16

    accuracy                           0.96        50
   macro avg       0.96      0.96      0.96        50
weighted avg       0.96      0.96      0.96        50

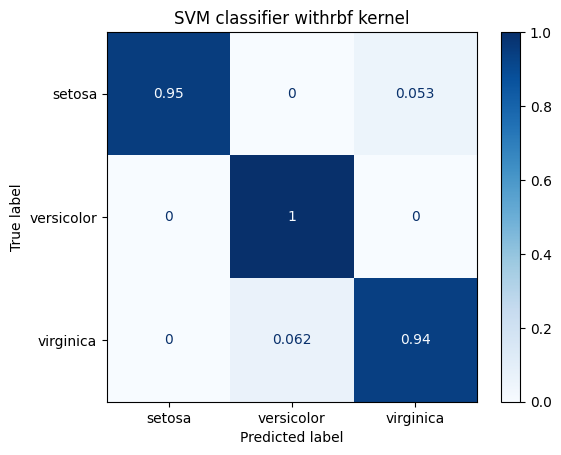
              precision    recall  f1-score   support

           0       1.00      1.00      1.00        19
           1       0.94      1.00      0.97        15
           2       1.00      0.94      0.97        16

    accuracy                           0.98        50
   macro avg       0.98      0.98      0.98        50
weighted avg       0.98      0.98      0.98        50

References

• Animate Your Own Fractals in Python with Matplotlib

• Arithmetic mean

• Geometric mean

• Harmonic mean

• Predicting sample size required for classification performance

• Cross entropy

• A Gentle Introduction to Cross-Entropy for Machine Learning

• Gradient Descent, the Learning Rate, and the importance of Feature Scaling

• Why is mean normalization useful in gradient descent?

• Feature scaling

• Normalizing your data (specifically, input and batch normalization)