Traitement de données massives
John Samuel
CPE Lyon
Année: 2024-2025
Courriel: john.samuel@cpe.fr

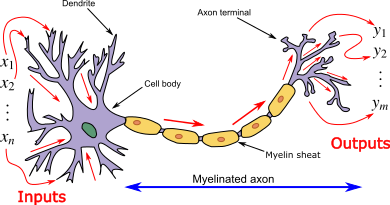

Les réseaux de neurones sont couramment utilisés dans le domaine de l'apprentissage machine, en particulier dans des tâches telles que la classification, la régression, la reconnaissance d'images, le traitement du langage naturel, et bien d'autres. Un réseau de neurones artificiels est une collection d'unités interconnectées appelées neurones artificiels. Ces réseaux sont inspirés de la structure du cerveau biologique
Les neurones sont organisés en couches. Il existe généralement trois types de couches dans un réseau de neurones :
L'objectif global de l'entraînement est d'ajuster les poids du réseau de manière à ce qu'il puisse généraliser à de nouvelles données, produisant des résultats précis pour des exemples qu'il n'a pas vu pendant l'entraînement.
Chaque neurone artificiel a des entrées, qui peuvent être les valeurs caractéristiques d'un échantillon de données externe, et produit une seule sortie. Cette sortie peut être envoyée à plusieurs autres neurones, formant ainsi la structure interconnectée du réseau neuronal. La fonction d'activation joue un rôle crucial dans le calcul de la sortie d'un neurone. Le processus comprend les étapes suivantes :
Connexions et poids: Le réseau de neurones est constitué de connexions, où chaque connexion transmet la sortie d'un neurone comme entrée à un autre neurone. Chaque connexion possède un poids qui représente son importance relative dans la transmission du signal.
Calcul de l'entrée d'un neurone : La fonction de propagation calcule l'entrée d'un neurone en prenant la somme pondérée des sorties de ses prédécesseurs, où chaque sortie est multipliée par le poids de la connexion correspondante. Cela peut être représenté mathématiquement comme suit :
\[ \text{Entrée du Neurone} = \sum_{i=1}^{n} (\text{Sortie du Prédécesseur}_i \times \text{Poids}_i) \] où \(n\) est le nombre de connexions d'entrée.
Ajout d'un terme de biais : Un terme de biais peut être ajouté au résultat de la propagation. Le terme de biais est un paramètre supplémentaire, souvent représenté par \(b\) dans les équations, qui permet au modèle d'apprendre un décalage ou une translation. Cela donne la forme finale de l'entrée du neurone :
\[ \text{Entrée du Neurone} = \sum_{i=1}^{n} (\text{Sortie du Prédécesseur}_i \times \text{Poids}_i) + \text{Biais} \]
Fonction d'Activation : Après avoir calculé l'entrée du neurone, celle-ci est passée à travers une fonction d'activation. Cette fonction introduit une non-linéarité dans le modèle, permettant au réseau de neurones de capturer des relations complexes et d'apprendre des modèles non linéaires. Certaines des fonctions d'activation couramment utilisées comprennent :
Le perceptron est un algorithme d'apprentissage supervisé utilisé pour la classification binaire. Il est conçu pour résoudre des problèmes où l'objectif est de déterminer si une entrée donnée appartient ou non à une classe particulière.

Le perceptron utilise généralement une fonction d'activation simple, et la fonction d'échelon (step function) est fréquemment choisie pour cette tâche.
La fonction d'échelon attribue une sortie de 1 si la somme pondérée des entrées dépasse un certain seuil, et 0 sinon.
\( f(x) = \begin{cases} 1 & \text{si } x \geq \text{seuil} \\ 0 & \text{sinon} \end{cases} \)
\[f(x)=x\]
\[f'(x)=1\]
\[f(x) = \begin{cases} 0 & \text{for } x < 0\\ 1 & \text{for } x \ge 0 \end{cases} \]
\[f'(x) = \begin{cases} 0 & \text{for } x \ne 0\\ ? & \text{for } x = 0\end{cases}\]
\[f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\]
\[f'(x)=f(x)(1-f(x))\]
\[f(x)=\tanh(x)=\frac{(e^{x} - e^{-x})}{(e^{x} + e^{-x})}\]
\[f'(x)=1-f(x)^2\]
\[f(x) = \begin{cases} 0 & \text{for } x \le 0\\ x & \text{for } x > 0\end{cases} = \max\{0,x\}= x \textbf{1}_{x>0}\]
\[f'(x) = \begin{cases} 0 & \text{for } x \le 0\\ 1 & \text{for } x > 0\end{cases}\]
\[f(x)=e^{-x^2}\]
\[f'(x)=-2xe^{-x^2}\]
Un réseau de neurones profond, également connu sous le nom de réseau de neurones profondément hiérarchisé ou réseau neuronal profond (DNN pour Deep Neural Network en anglais), est un type de réseau de neurones artificiels qui comprend plusieurs couches de traitement, généralement plus de deux. Ces réseaux sont appelés "profonds" en raison de leur architecture empilée de couches, permettant la création de représentations hiérarchiques complexes des données.
Architecture en couches : Les réseaux de neurones profonds sont composés de multiples couches, généralement divisées en trois types principaux :
L'entraînement de réseaux de neurones profonds peut nécessiter des volumes importants de données et de puissance de calcul.
# Importation des bibliothèques nécessaires de TensorFlow
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD
# Étape 1: Création d'un modèle séquentiel
model = Sequential()
# Étape 2: Ajout d'une couche dense avec une fonction d'activation ReLU
# La couche a 4 neurones, une fonction d'activation 'relu', et prend une entrée de forme (3,)
model.add(Dense(4, activation='relu', input_shape=(3,)))
# Étape 3: Ajout d'une couche dense de sortie avec une fonction d'activation softmax
# La couche a 2 neurones pour une tâche de classification binaire, et softmax est utilisé
# pour obtenir des probabilités
model.add(Dense(units=2, activation='softmax'))
# Étape 4: Compilation du modèle
# Utilisation de la descente de gradient stochastique (SGD) comme optimiseur avec un taux d'apprentissage de 0.01
# La fonction de perte est 'mean_squared_error' pour un problème de régression
# Les performances du modèle seront mesurées en termes de 'accuracy' (précision)
sgd = SGD(lr=0.01)
model.compile(loss='mean_squared_error', optimizer=sgd, metrics=['accuracy'])
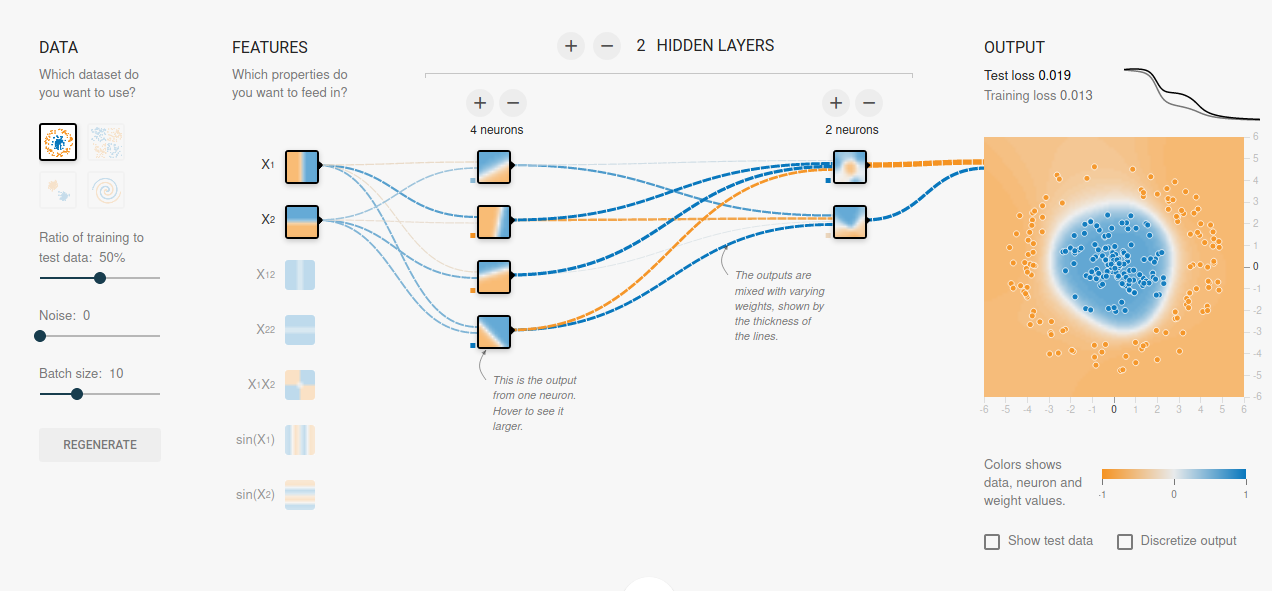
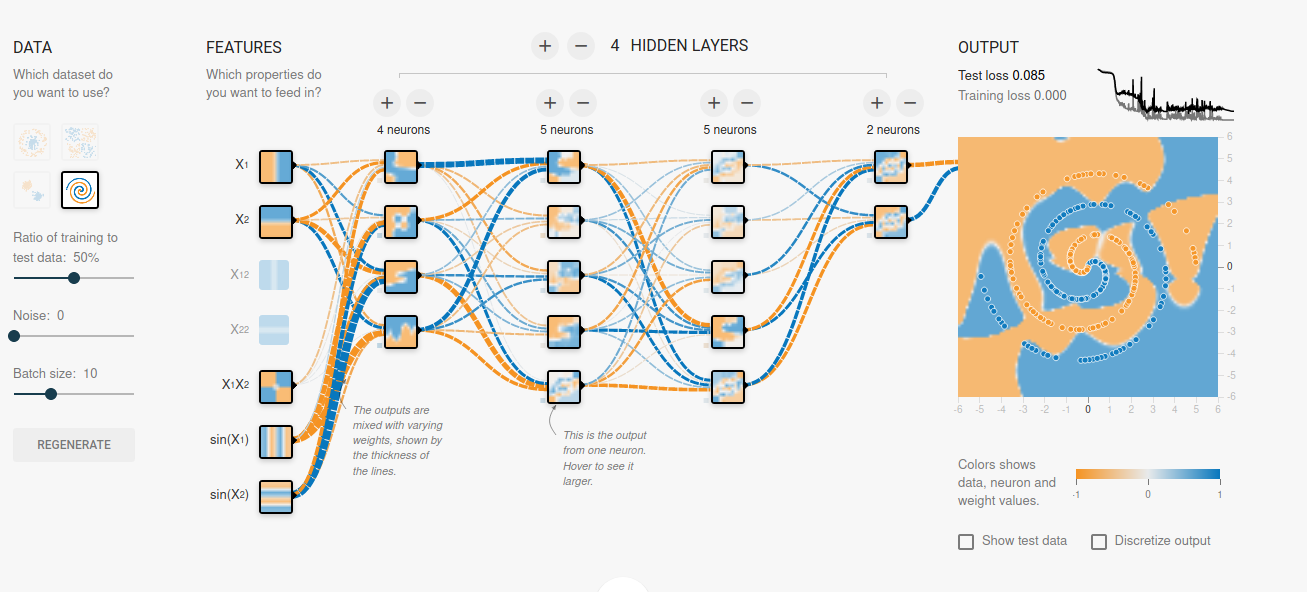
Un réseau de neurones profond est une architecture complexe où l'information circule de la couche d'entrée à travers les couches cachées jusqu'à la couche de sortie. Chaque connexion entre les neurones est associée à un poids qui est ajusté pendant le processus d'apprentissage pour optimiser les performances du modèle sur la tâche spécifique. L'utilisation de plusieurs couches cachées permet au réseau d'apprendre des représentations de plus en plus abstraites et complexes des données.
Connectivité entièrement connectée: Dans une connectivité entièrement connectée, chaque neurone d'une couche est connecté à chaque neurone de la couche suivante. Cela signifie que toutes les informations de la couche précédente sont transmises à chaque neurone de la couche suivante. C'est la configuration la plus courante dans les couches totalement connectées, généralement présentes dans les parties du réseau proches de la sortie.
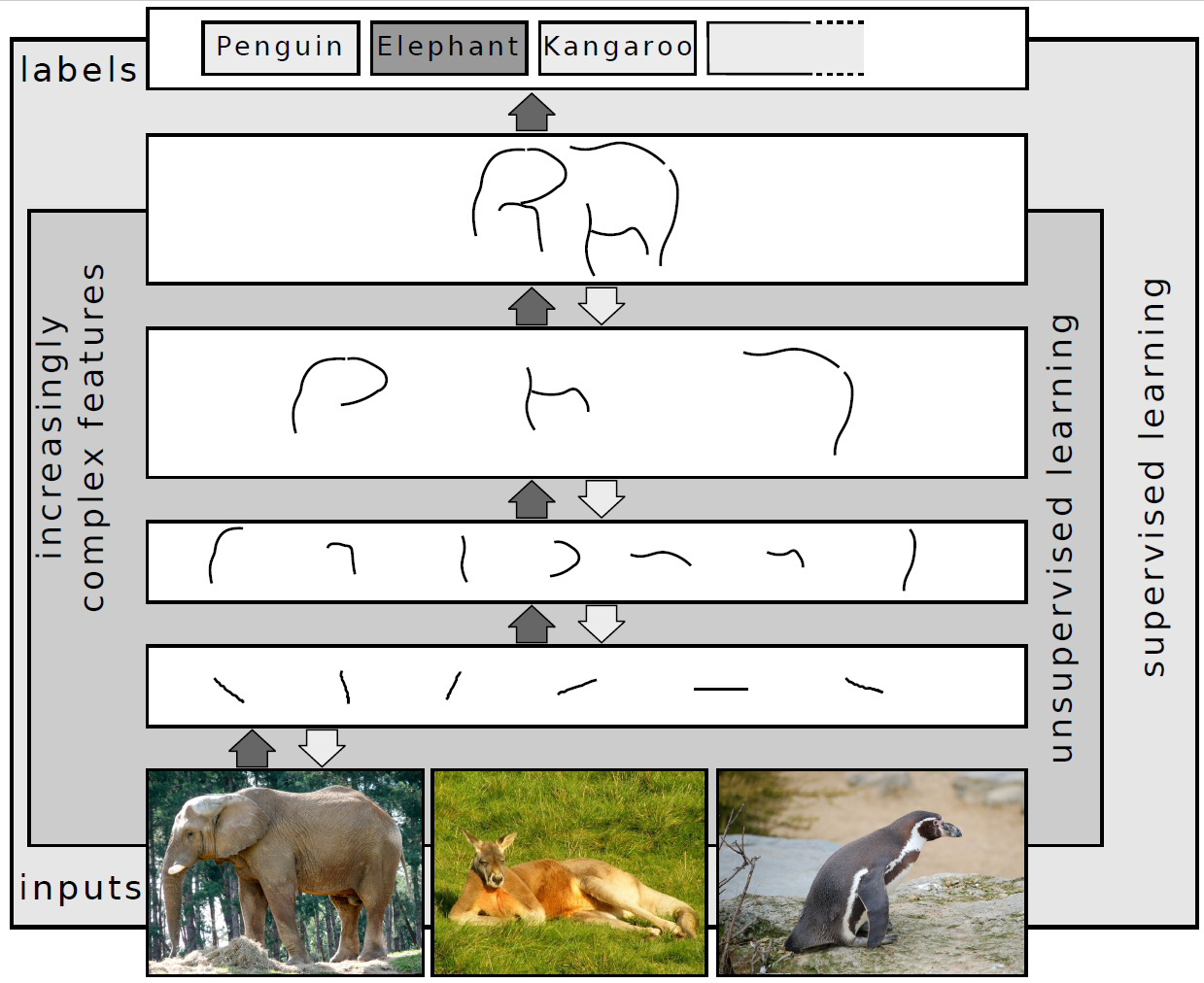
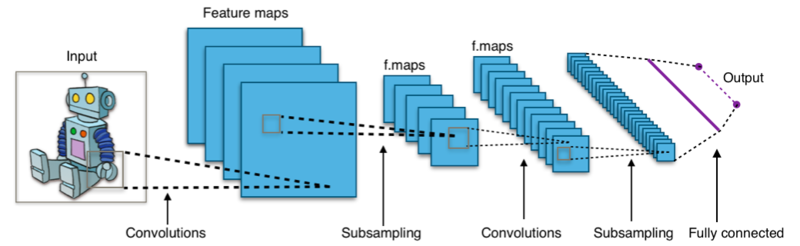
Les réseaux de neurones convolutionnels (CNN) sont une classe d'architectures de réseaux neuronaux conçues principalement pour l'analyse des images. Ils ont été particulièrement efficaces dans des tâches telles que la classification d'images, la détection d'objets, et la segmentation d'images.

En résumé, les CNN suivent une architecture hiérarchique, où les couches convolutives apprennent des caractéristiques locales, et ces caractéristiques sont ensuite combinées dans les couches suivantes pour former des représentations plus complexes. La non-linéarité introduite par la fonction d'activation ReLU est cruciale pour permettre au modèle d'apprendre des relations non linéaires dans les données.
Un noyau dans le contexte du traitement d'images, également appelé filtre ou masque, est une petite matrice qui est appliquée sur une image à l'aide d'une opération de convolution. L'objectif de l'application de ces noyaux est de réaliser diverses opérations de filtrage sur l'image, telles que la détection de contours, l'amélioration des détails, la mise en évidence de certaines caractéristiques, etc.