Intelligence artificielle et Deep Learning

Apprentissage profond

John Samuel
CPE Lyon

Année: 2024-2025
Courriel: john.samuel@cpe.fr

Perceptron simple couche

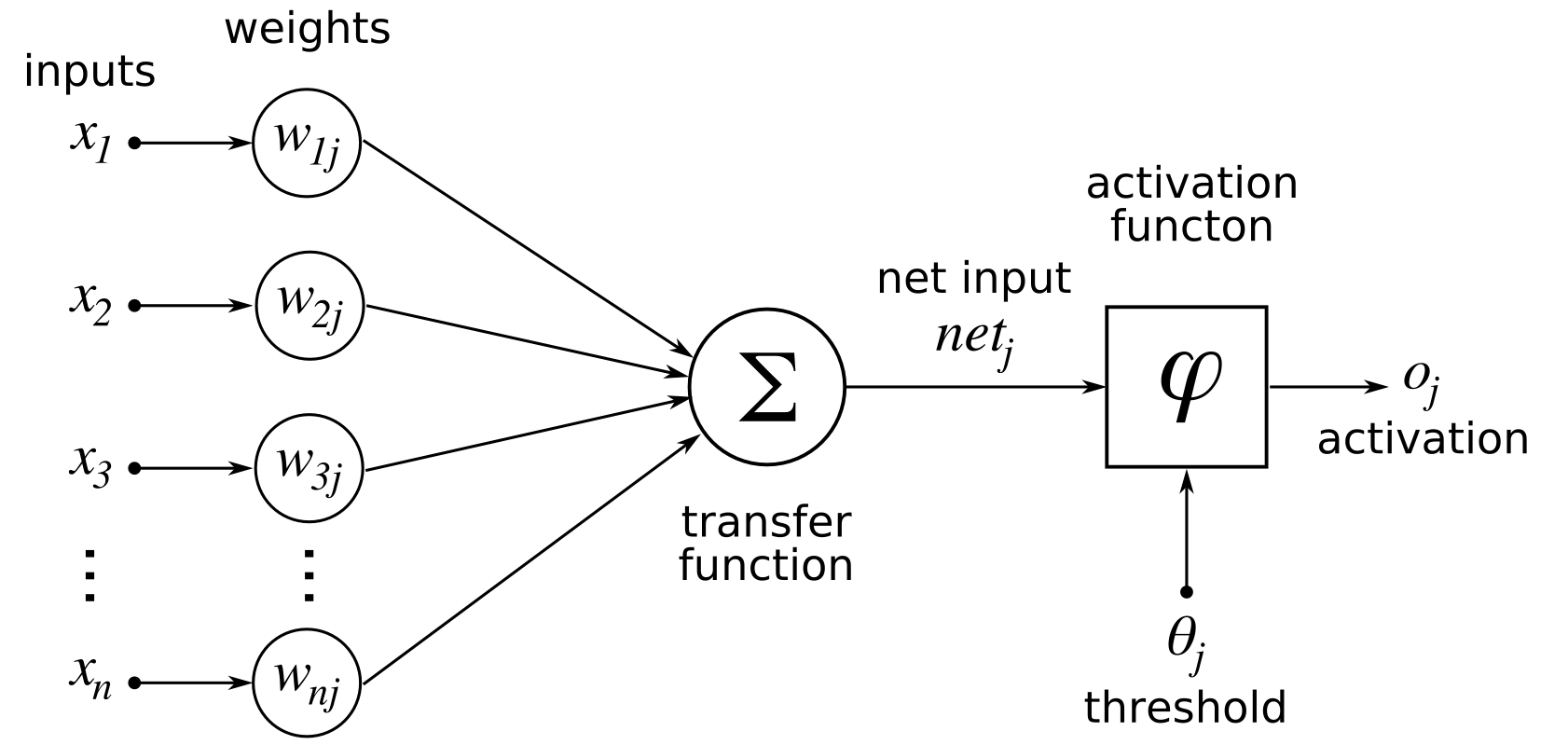
Le perceptron à simple couche, bien qu'il ait été une avancée significative dans le développement des réseaux de neurones artificiels, présente certaines limites importantes qui restreignent sa capacité à résoudre des problèmes complexes. Voici quelques-unes des principales limitations du perceptron à simple couche :

Linéarité : Le perceptron à simple couche ne peut apprendre que des fonctions linéaires. Il ne peut pas capturer des relations non linéaires complexes dans les données. Les problèmes qui ne peuvent pas être résolus avec des frontières de décision linéaires dépassent les capacités du perceptron à simple couche.
Incapacité à résoudre le problème XOR : L'une des limitations emblématiques du perceptron à simple couche est son incapacité à résoudre le problème XOR (ou des problèmes similaires non linéaires). En raison de sa nature linéaire, il ne peut pas séparer correctement les exemples positifs et négatifs du XOR.
Sensibilité aux données déséquilibrées : Le perceptron à simple couche peut être sensible aux données déséquilibrées, où une classe a significativement plus d'exemples que l'autre. Cela peut conduire à des difficultés lors de l'apprentissage, surtout si la classe minoritaire est mal représentée.

Perceptron simple couche

Uniquement pour des tâches de classification binaire : Le perceptron à simple couche est limité à des tâches de classification binaire. Il ne peut pas être directement étendu pour traiter des tâches de classification multiclasse sans des modifications supplémentaires.
Dépendance aux caractéristiques linéaires : Les résultats du perceptron dépendent fortement de la linéarité des caractéristiques. Si les caractéristiques ne sont pas linéaires, le perceptron ne peut pas les exploiter efficacement pour faire des prédictions précises.
Manque de capacité d'apprentissage hiérarchique : Le perceptron à simple couche ne peut pas apprendre des représentations hiérarchiques des données. Les réseaux de neurones profonds, avec plusieurs couches cachées, sont capables de capturer des caractéristiques à différents niveaux d'abstraction.
Sensibilité aux valeurs aberrantes : Le perceptron simple couche peut être sensible aux valeurs aberrantes (outliers) dans les données, ce qui peut affecter négativement ses performances.

Pour surmonter ces limitations, des architectures plus complexes telles que les réseaux de neurones profonds avec plusieurs couches cachées ont été développées. Ces réseaux permettent une représentation plus riche et non linéaire des données, rendant possible la résolution de problèmes plus complexes.

Perceptron multicouche

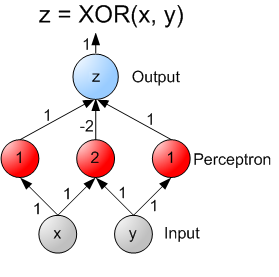
Le perceptron multicouche, également appelé réseau de neurones à plusieurs couches, surmonte plusieurs des limitations du perceptron à simple couche en introduisant des couches cachées et des fonctions d'activation non linéaires.

Capacité à modéliser des relations non linéaires : Contrairement au perceptron à simple couche, le perceptron multicouche est capable de capturer des relations non linéaires complexes dans les données. Les couches cachées et les fonctions d'activation non linéaires permettent d'apprendre des représentations plus riches.
Apprentissage hiérarchique : Le perceptron multicouche a la capacité d'apprendre des représentations hiérarchiques des données. Les différentes couches cachées peuvent extraire des caractéristiques à différents niveaux d'abstraction.

Perceptron multicouche

Adaptabilité à des tâches complexes : Il est plus adapté pour des tâches complexes telles que la vision par ordinateur, la reconnaissance vocale, la traduction automatique, etc., où les relations dans les données sont souvent non linéaires.
Gestion de données déséquilibrées : Le perceptron multicouche peut mieux gérer les problèmes de données déséquilibrées en raison de sa capacité à apprendre des représentations complexes.
Tâches de classification multiclasse : Il peut être utilisé pour des tâches de classification multiclasse sans modification majeure.
Adaptabilité à diverses fonctions d'activation : Il peut utiliser différentes fonctions d'activation dans différentes couches, ce qui augmente sa flexibilité pour modéliser des relations complexes.

Réseau de Neurones Profond

Le terme "profond" se réfère à un réseau qui a un grand nombre de couches, généralement plus de trois.
Ces réseaux sont également appelés "réseaux de neurones profonds" ou "réseaux neuronaux profonds".
Les réseaux de neurones profonds ont été rendus populaires par leurs capacités à apprendre des représentations hiérarchiques complexes.

Exemple: Tensorflow

# Importation des bibliothèques nécessaires de TensorFlow
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.optimizers import SGD

# Étape 1: Création d'un modèle séquentiel
model = Sequential()

# Étape 2: Ajout d'une couche dense avec une fonction d'activation ReLU
# La couche a 4 neurones, une fonction d'activation 'relu', et prend une entrée de forme (3,)
model.add(Dense(4, activation='relu', input_shape=(3,)))

Exemple: Tensorflow

# Étape 3: Ajout d'une couche dense de sortie avec une fonction d'activation softmax
# La couche a 2 neurones pour une tâche de classification binaire, et softmax est utilisé
# pour obtenir des probabilités
model.add(Dense(units=2, activation='softmax'))

# Étape 4: Compilation du modèle
# Utilisation de la descente de gradient stochastique (SGD) comme optimiseur avec un taux d'apprentissage de 0.01
# La fonction de perte est 'mean_squared_error' pour un problème de régression
# Les performances du modèle seront mesurées en termes de 'accuracy' (précision)
sgd = SGD(lr=0.01)
model.compile(loss='mean_squared_error', optimizer=sgd, metrics=['accuracy'])

Étape 1: On crée un modèle séquentiel, qui est une pile linéaire de couches.
Étape 2: On ajoute une couche dense avec 4 neurones utilisant la fonction d'activation ReLU. La couche prend une entrée de forme (3,) - cela signifie que chaque exemple d'entraînement a trois caractéristiques.
Étape 3: On ajoute une couche dense de sortie avec 2 neurones utilisant la fonction d'activation softmax. Cela est couramment utilisé pour les tâches de classification binaire, fournissant des probabilités pour chaque classe.
Étape 4: On compile le modèle en spécifiant l'optimiseur (SGD avec un taux d'apprentissage de 0.01), la fonction de perte ('mean_squared_error' pour une tâche de régression), et les métriques de performance ('accuracy' pour mesurer la précision du modèle).

Source: https://playground.tensorflow.org/

import numpy as np
import tensorflow as tf
from tensorflow.keras.callbacks import EarlyStopping, ModelCheckpoint
from tensorflow.keras.layers import Dense
from tensorflow.keras.models import Sequential
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder
from sklearn.datasets import load_iris
import matplotlib.pyplot as plt

# 1. Préparation des données
# Charger le jeu de données IRIS
data = load_iris()
X = data.data  # Les caractéristiques
y = data.target.reshape(-1, 1)  # Les étiquettes

# Encodage en one-hot des étiquettes
encoder = OneHotEncoder(sparse_output=False)
y_encoded = encoder.fit_transform(y)

# Division en ensembles d'entraînement et de test
X_train, X_test, y_train, y_test = train_test_split(X, y_encoded, test_size=0.2, random_state=42)

# Normalisation des données
mean = X_train.mean(axis=0)
std = X_train.std(axis=0)
X_train = (X_train - mean) / std
X_test = (X_test - mean) / std

# 2. Création du modèle
model = Sequential([
    Dense(10, activation='relu', input_shape=(X.shape[1],)),
    Dense(10, activation='relu'),
    Dense(3, activation='softmax')
])

# Compilation du modèle
model.compile(optimizer='adam',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

# 3. Définition des callbacks
# Arrêt anticipé pour éviter le surapprentissage
early_stopping = EarlyStopping(monitor='val_loss', patience=5, restore_best_weights=True)

# Sauvegarde du meilleur modèle
checkpoint = ModelCheckpoint('best_model.keras', monitor='val_loss', save_best_only=True)

# 4. Entraînement du modèle
history = model.fit(X_train, y_train,
                    validation_split=0.2,
                    epochs=100,
                    batch_size=4,
                    callbacks=[early_stopping, checkpoint])

# 5. Évaluation du modèle
test_loss, test_accuracy = model.evaluate(X_test, y_test)
print(f"Test Loss: {test_loss:.4f}")
print(f"Test Accuracy: {test_accuracy:.4f}")

# 6. Visualisation des performances
# Visualisation de la courbe de perte et de précision
plt.figure(figsize=(12, 5))

# Courbe de perte
plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Courbe de perte')
plt.legend()

# Courbe de précision
plt.subplot(1, 2, 2)
plt.plot(history.history['accuracy'], label='Train Accuracy')
plt.plot(history.history['val_accuracy'], label='Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title('Courbe de précision')
plt.legend()

plt.show()

# 7. Chargement du meilleur modèle sauvegardé et prédiction
best_model = tf.keras.models.load_model('best_model.keras')

# Prédiction sur les données de test
y_pred = best_model.predict(X_test)
y_pred_classes = np.argmax(y_pred, axis=1)
y_true_classes = np.argmax(y_test, axis=1)

# Affichage de quelques prédictions pour vérifier le modèle
print("Vraies classes:", y_true_classes)
print("Classes prédites:", y_pred_classes)

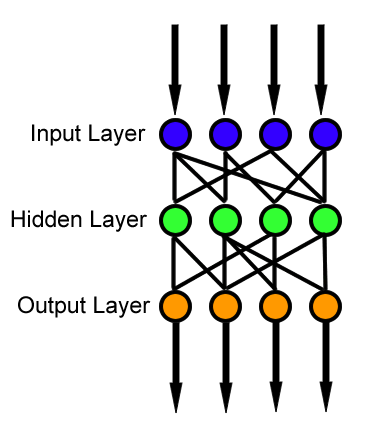
Composants des réseaux de neurones artificiels

Organisation

Un réseau de neurones profond est une architecture complexe où l'information circule de la couche d'entrée à travers les couches cachées jusqu'à la couche de sortie. Chaque connexion entre les neurones est associée à un poids qui est ajusté pendant le processus d'apprentissage pour optimiser les performances du modèle sur la tâche spécifique. L'utilisation de plusieurs couches cachées permet au réseau d'apprendre des représentations de plus en plus abstraites et complexes des données.

Organisation en plusieurs couches : Un réseau de neurones profond est structuré en plusieurs couches, généralement composées d'une couche d'entrée, de plusieurs couches cachées et d'une couche de sortie. Chaque couche est composée de neurones, également appelés nœuds ou unités.
Connexions entre les neurones : Les neurones d'une couche sont connectés aux neurones de la couche immédiatement précédente et de la couche immédiatement suivante. Chaque connexion est associée à un poids qui est ajusté pendant l'apprentissage.

Composants des réseaux de neurones artificiels

Organisation

Couche d'entrée : La couche d'entrée est la première couche du réseau. Elle reçoit les données externes, souvent représentées par des caractéristiques d'un ensemble de données. Chaque neurone dans la couche d'entrée correspond à une caractéristique spécifique.
Couche de sortie : La couche de sortie est la dernière couche du réseau. Elle produit le résultat final du modèle en fonction de la tâche spécifique, telle que la classification d'une image, la prédiction d'une valeur, etc. Le nombre de neurones dans cette couche dépend du type de problème (par exemple, un neurone pour chaque classe dans une tâche de classification).
Couches cachées : Entre la couche d'entrée et la couche de sortie, il peut y avoir zéro ou plusieurs couches cachées. Ces couches sont responsables de l'extraction de caractéristiques complexes à partir des données d'entrée. Chaque neurone dans une couche cachée combine les informations des neurones de la couche précédente pour apprendre des représentations hiérarchiques.

Composants des réseaux de neurones artificiels

Organisation et connectivité

Connectivité entièrement connectée: Dans une connectivité entièrement connectée, chaque neurone d'une couche est connecté à chaque neurone de la couche suivante. Cela signifie que toutes les informations de la couche précédente sont transmises à chaque neurone de la couche suivante. C'est la configuration la plus courante dans les couches totalement connectées, généralement présentes dans les parties du réseau proches de la sortie.

Composants des réseaux de neurones artificiels

Organisation et connectivité

Connectivité par le biais de la mise en commun (Pooling)

Le pooling est une opération souvent utilisée pour réduire la dimension des cartes de caractéristiques tout en préservant les informations essentielles. Dans le contexte de la connectivité, un groupe de neurones dans une couche peut être connecté à un seul neurone dans la couche suivante.
Il existe différents types de pooling, comme le pooling max et le pooling moyen. Dans le pooling max, par exemple, chaque groupe de neurones transmet uniquement l'activation maximale à un neurone dans la couche suivante. Cela réduit le nombre de neurones, ce qui peut être utile pour la gestion de la complexité computationnelle et la réduction du surapprentissage.

Composants des réseaux de neurones artificiels

Organisation et connectivité

Réseaux de Neurones en Aval (Feedforward Neural Networks) :

Les réseaux de neurones en aval, également appelés réseaux feedforward, ne permettent pas de cycles entre les couches. L'information circule dans une seule direction, de la couche d'entrée à la couche de sortie, sans boucles récurrentes. Chaque couche traite indépendamment les données et transmet les résultats à la couche suivante.
Ces réseaux sont couramment utilisés pour des tâches où les données peuvent être traitées de manière indépendante, comme la classification d'images, la reconnaissance vocale, etc.

Les réseaux de neurones en aval, sont plus adaptés à des tâches où chaque exemple de données peut être traité de manière indépendante.

Composants des réseaux de neurones artificiels

Organisation et connectivité

Réseaux Récurrents

Les réseaux récurrents permettent des connexions entre les neurones de la même couche ou des couches précédentes. Cela signifie qu'ils ont des boucles ou des connexions récurrentes, permettant aux informations de circuler à travers le réseau de manière répétée. Ces connexions récurrentes permettent aux réseaux récurrents de prendre en compte les séquences et les dépendances temporelles dans les données.
Les réseaux récurrents sont souvent utilisés pour traiter des données séquentielles telles que des séquences temporelles, des phrases dans le traitement du langage naturel (NLP), etc.

La connectivité récurrente dans les réseaux récurrents permet aux informations de persister et d'être mises à jour à chaque itération ou pas de temps, ce qui les rend adaptés à des tâches séquentielles.

Réseaux de neurones artificiels: Hyperparamètres

Les hyperparamètres sont des paramètres constants dont la valeur est fixée avant le début du processus d'apprentissage d'un réseau de neurones artificiels. Contrairement aux paramètres du modèle, qui sont appris pendant l'entraînement, les hyperparamètres sont des choix de conception qui influencent la manière dont le modèle est formé. Voici quelques exemples d'hyperparamètres couramment utilisés dans les réseaux de neurones :

Taux d'apprentissage : Le taux d'apprentissage contrôle la taille des pas que l'algorithme d'optimisation prend pour ajuster les poids du modèle. Un taux d'apprentissage trop élevé peut entraîner une convergence rapide mais peut sauter le minimum global, tandis qu'un taux d'apprentissage trop bas peut rendre l'apprentissage lent ou susceptible de rester coincé dans des minima locaux.

Réseaux de neurones artificiels: Hyperparamètres

Nombre de couches cachées : Le nombre de couches cachées dans le réseau de neurones est un choix de conception important. Il influe sur la capacité du modèle à apprendre des représentations complexes. Un modèle avec plus de couches cachées peut capturer des caractéristiques plus abstraites, mais cela peut également augmenter la complexité du modèle et entraîner un surapprentissage.
Taille des échantillons (Batch Size) : La taille des échantillons détermine le nombre d'exemples d'entraînement utilisés pour mettre à jour les poids du modèle à chaque itération. Un choix judicieux de la taille des échantillons peut influencer l'efficacité de l'entraînement et la stabilité du modèle.
Fonction d'activation : La fonction d'activation est utilisée pour introduire de la non-linéarité dans le modèle. Des choix courants incluent ReLU, Sigmoid, et Tanh. Le choix de la fonction d'activation peut affecter la capacité du modèle à apprendre des relations complexes.

Réseaux de neurones artificiels: Hyperparamètres

Régularisation : Les techniques de régularisation, telles que la régularisation L1 ou L2, ajoutent des termes de pénalité aux poids du modèle pour prévenir le surapprentissage. Le choix et la force de la régularisation sont des hyperparamètres importants.
Nombre de neurones par couche : Le nombre de neurones dans chaque couche, en particulier dans les couches cachées, influence la capacité du modèle à apprendre des représentations spécifiques. Un choix judicieux peut aider à contrôler la complexité du modèle.
Optimiseur (Optimizer) : L'algorithme d'optimisation qui ajuste les poids du réseau lors de la rétropropagation. Des exemples incluent SGD, Adam, RMSprop.

Réseaux de neurones artificiels: Hyperparamètres

Initialisation des poids : Méthode utilisée pour initialiser les poids du réseau avant l'entraînement. Des méthodes courantes incluent l'initialisation aléatoire et l'initialisation Xavier/Glorot.
Fonction de perte (Loss Function) : La fonction qui mesure la différence entre les prédictions du modèle et les vraies valeurs. Elle guide l'ajustement des poids lors de l'entraînement.
Taux de drop-out (Dropout Rate) : Le nombre de fois que l'ensemble de données complet est passé à travers le réseau pendant l'entraînement.
Nombre d'époques (Epochs) : Le nombre de neurones dans chaque couche, en particulier dans les couches cachées, influence la capacité du modèle à apprendre des représentations spécifiques. Un choix judicieux peut aider à contrôler la complexité du modèle.
Moments (Momentum) : Paramètre qui accélère l'optimisation en ajoutant une fraction de l'itération précédente au poids actuel lors de la mise à jour.

Réseaux de neurones artificiels: Hyperparamètres

Taille de la fenêtre de convolution (Convolutional Window Size) : Pour les réseaux de neurones convolutifs (CNN), la taille de la fenêtre utilisée pour la convolution.
Pas de la fenêtre de convolution (Convolutional Stride) : : Le nombre d'unités entre chaque opération de convolution dans un CNN.
Taille de la fenêtre de pooling (Pooling Window Size) : : Pour les CNN, la taille de la fenêtre utilisée pour l'opération de pooling.

Réseaux de neurones artificiels: Hyperparamètres

Arrêt anticipé (Early Stopping) : Une technique qui consiste à arrêter l'entraînement du modèle dès que la performance sur un ensemble de validation cesse de s'améliorer, afin d'éviter le surajustement.
Répartition Entraînement vs. Validation (Training vs. Validation Split) : La division de l'ensemble de données en ensembles distincts d'entraînement et de validation pour évaluer les performances du modèle pendant l'entraînement.
Augmentation de données (Data Augmentation) : La création de nouvelles données d'entraînement en appliquant des transformations telles que la rotation, le redimensionnement, le décalage, etc., pour augmenter la diversité de l'ensemble de données.

Réseaux de neurones artificiels: Hyperparamètres

Prétraitement des données (Data Preprocessing) : Les transformations appliquées aux données d'entrée avant de les fournir au réseau, telles que la normalisation, la standardisation, le redimensionnement, etc.
Modèles pré-entraînés (Pretrained Models) : L'utilisation de modèles déjà entraînés sur de grandes bases de données (comme ImageNet pour les modèles de vision par ordinateur) comme point de départ pour des tâches spécifiques.

Le réglage judicieux de ces hyperparamètres est souvent crucial pour obtenir des performances optimales d'un modèle de réseau de neurones. Il implique souvent des expérimentations et des ajustements itératifs pour trouver la combinaison optimale pour une tâche d'apprentissage spécifique.

Réseaux de neurones artificiels: Hyperparamètres

Réseaux	Nombre de couches
AlexNet	8
VGGNet	16
InceptionNet	27
GoogleNet	22
ResNet	50, 101, 152, 200, 345
DenseNet	121, 169, 201
MobileNetV2	13, 16, 23

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones profonds

ReLU (Rectified Linear Unit) :La fonction ReLU est largement utilisée en raison de sa simplicité et de sa capacité à introduire une non-linéarité. Elle remplace les valeurs négatives par zéro, permettant au réseau d'apprendre des représentations complexes. \[f(x) = \max(0, x)\]

Sigmoid : Souvent utilisée en couche de sortie pour les problèmes de classification binaire, car elle ramène les valeurs à l'intervalle [0, 1], pouvant être interprétées comme des probabilités. \[f(x) = \frac{1}{1 + e^{-x}}\]

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones profonds

Tanh (Tangente hyperbolique) : Similaire à la fonction sigmoïde, mais ramène les valeurs à l'intervalle [-1, 1]. Elle est souvent utilisée en tant que fonction d'activation pour les couches cachées. \[f(x) = \frac{e^{2x} - 1}{e^{2x} + 1}\]

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones profonds

Softmax : Principalement utilisée en couche de sortie pour les problèmes de classification multiclasse. Elle transforme les scores en probabilités. \[f(x)_i = \frac{e^{x_i}}{\sum_{j}e^{x_j}}\] pour chaque \(i\)-ème élément du vecteur \(x\)

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones convolutifs (CNN)

ReLU (Rectified Linear Unit) : La fonction ReLU est également largement utilisée dans les CNN en raison de sa non-linéarité et de sa facilité de calcul
Leaky ReLU : Une variation de ReLU qui permet un petit gradient pour les valeurs négatives, aidant à atténuer certains problèmes liés à ReLU (neuron death). \[f(x) = \max(\alpha x, x)\] avec \(\alpha > 0\) (un petit coefficient)
Sigmoid et Tanh : Utilisées dans certaines situations, notamment en couche de sortie pour la classification binaire.
Softmax : Comme pour les DNN, elle est souvent utilisée en couche de sortie pour la classification multiclasse dans les CNN.

Réseaux de neurones artificiels: Hyperparamètres

Fonctions de perte

Les fonctions de perte (loss functions) sont des métriques qui mesurent à quel point les prédictions d'un modèle diffèrent des valeurs réelles attendues. Choisir la bonne fonction de perte dépend du type de problème que vous essayez de résoudre, qu'il s'agisse d'une tâche de classification, de régression, ou autre.

Fonction de Perte	Type de Problème	Utilisation
Mean Squared Error (MSE)	Régression	\( \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 \) - Mesure l'erreur quadratique moyenne entre les prédictions (\( \hat{y}_i \)) et les valeurs réelles (\( y_i \)). Utile lorsque les erreurs doivent être pénalisées de manière significative.

Réseaux de neurones artificiels: Hyperparamètres

Fonctions de perte

Fonction de Perte	Type de Problème	Utilisation
Mean Absolute Error (MAE)	Régression	\( \frac{1}{n} \sum_{i=1}^{n} \|y_i - \hat{y}_i\| \) - Mesure l'erreur absolue moyenne entre les prédictions (\( \hat{y}_i \)) et les valeurs réelles (\( y_i \)). Moins sensible aux valeurs aberrantes que le MSE.
Binary Crossentropy	Classification Binaire	\( -\frac{1}{n} \sum_{i=1}^{n} \left(y_i \cdot \log(\hat{y}_i) + (1-y_i) \cdot \log(1-\hat{y}_i)\right) \) - Fonction de perte pour la classification binaire. Convient lorsque chaque exemple d'entraînement appartient à une seule classe.

Réseaux de neurones artificiels: Hyperparamètres

Fonctions de perte

Fonction de Perte	Type de Problème	Utilisation
Categorical Crossentropy	Classification Multiclasse	\( -\frac{1}{n} \sum_{i=1}^{n} \sum_{j=1}^{m} y_{i,j} \cdot \log(\hat{y}_{i,j}) \) - Fonction de perte pour la classification multiclasse. Convient lorsque chaque exemple d'entraînement peut appartenir à plusieurs classes.
Hinge Loss	SVM (Support Vector Machine)	\( \frac{1}{n} \sum_{i=1}^{n} \max(0, 1 - y_i \cdot \hat{y}_i) \) - Utilisé pour les machines à vecteurs de support. Pénalise les erreurs lorsque la prédiction (\( \hat{y}_i \)) n'est pas du bon côté de la marge.

Réseaux de neurones artificiels: Hyperparamètres

Fonctions de perte

Fonction de Perte	Type de Problème	Utilisation
Huber Loss	Régression	\( \frac{1}{n} \sum_{i=1}^{n} L_{\delta}(y_i - \hat{y}_i) \) - Une combinaison de MSE et MAE. Moins sensible aux valeurs aberrantes que MSE et moins impacté par celles-ci que MAE.
Poisson Loss	Régression (Poisson)	\( \frac{1}{n} \sum_{i=1}^{n} \left(\hat{y}_i - y_i \cdot \log(\hat{y}_i) \right) \) - Utilisé pour des tâches de régression où les valeurs suivent une distribution de Poisson.

Réseaux de neurones artificiels: Hyperparamètres

Optimiseurs

Optimiseur	Description
Stochastic Gradient Descent (SGD)	L'optimiseur de descente de gradient stochastique classique. Il met à jour les poids du modèle en se déplaçant dans la direction opposée du gradient moyen calculé sur un petit lot de données d'entraînement à la fois.
Adam (Adaptive Moment Estimation)	Un optimiseur qui combine des idées de RMSprop et de Momentum. Il adapte les taux d'apprentissage des paramètres en fonction de leurs gradients moyens et de leurs moments moyens. Très populaire et souvent recommandé pour de nombreuses tâches.

Réseaux de neurones artificiels: Hyperparamètres

Optimiseurs

Optimiseur	Description
RMSprop (Root Mean Square Propagation)	Ajuste les taux d'apprentissage pour chaque paramètre individuellement en utilisant une moyenne pondérée exponentielle des carrés des gradients. Cela aide à atténuer les problèmes liés aux taux d'apprentissage dans la descente de gradient stochastique.

Un réseau de neurones profond, également connu sous le nom de réseau de neurones profondément hiérarchisé ou réseau neuronal profond (DNN pour Deep Neural Network en anglais), est un type de réseau de neurones artificiels qui comprend plusieurs couches de traitement, généralement plus de deux. Ces réseaux sont appelés "profonds" en raison de leur architecture empilée de couches, permettant la création de représentations hiérarchiques complexes des données.

Architecture en couches : Les réseaux de neurones profonds sont composés de multiples couches, généralement divisées en trois types principaux :

Couche d'Entrée : Reçoit les données brutes ou caractéristiques en entrée.
Couches Cachées : Effectuent des transformations non linéaires et apprennent des représentations hiérarchiques des données.
Couche de Sortie : Produit la sortie du réseau, adaptée à la tâche spécifique (classification, régression, etc.).

Apprentissage Hiérarchique : Les couches cachées d'un réseau de neurones profond apprennent des caractéristiques de plus en plus abstraites et complexes à mesure que l'on progresse en profondeur. Chaque couche représente une abstraction des caractéristiques extraites par les couches précédentes.
Fonctions d'Activation : Des fonctions d'activation non linéaires, telles que ReLU (Rectified Linear Unit) ou ses variantes, sont couramment utilisées dans les couches cachées pour permettre au réseau d'apprendre des relations non linéaires.
Apprentissage Profond : L'apprentissage profond implique l'ajustement simultané des poids de toutes les couches du réseau pour minimiser l'erreur de prédiction. Cela est généralement réalisé en utilisant des techniques de rétropropagation et de descente de gradient.
Utilisations : Les réseaux de neurones profonds sont utilisés dans une variété de tâches, notamment la vision par ordinateur, la reconnaissance vocale, le traitement du langage naturel, la traduction automatique, la recommandation de contenu, et bien d'autres. Leur capacité à apprendre des représentations complexes a conduit à des avancées significatives dans de nombreux domaines de l'intelligence artificielle.

L'entraînement de réseaux de neurones profonds peut nécessiter des volumes importants de données et de puissance de calcul.

Il existe plusieurs types de réseaux de neurones profonds.

Réseaux de Neurones Convolutionnels (CNN) :
- Utilisation Principale : Vision par ordinateur, reconnaissance d'images.
- Caractéristiques : Les CNN sont efficaces pour extraire des motifs spatiaux à partir d'images en utilisant des opérations de convolution. Ils sont largement utilisés dans des applications telles que la classification d'images, la détection d'objets et la segmentation d'images.
Réseaux de Neurones Récurrents (RNN) :
- Utilisation Principale : Traitement de séquences, traitement du langage naturel.
- Caractéristiques : Les RNN sont conçus pour traiter des données séquentielles en utilisant des connexions récurrentes qui leur permettent de conserver une mémoire à long terme. Ils sont utilisés pour des tâches telles que la traduction automatique, la génération de texte et l'analyse de séquences temporelles.

Réseaux de Neurones Générateurs Adverses (GAN) :
- Utilisation Principale : Génération d'images réalistes.
- Caractéristiques : Les GAN sont composés de deux réseaux, un générateur et un discriminateur, qui s'entraînent de manière adversaire. Les GAN sont utilisés pour générer des données réalistes, y compris des images, des vidéos et du son.
Réseaux de Neurones Résiduels (ResNet) :
- Utilisation Principale : Classification d'images profondes.
- Caractéristiques : Les architectures ResNet utilisent des connexions résiduelles pour faciliter l'apprentissage profond en surmontant le problème du "vanishing gradient". Ils sont fréquemment utilisés dans des compétitions de classification d'images.

Autoencodeurs et Variational Autoencoders (VAE) :
- Utilisation Principale : Compression et génération de données.
- Caractéristiques : Les autoencodeurs sont utilisés pour apprendre des représentations compactes de données en comprimant et en reconstruisant les informations. Les VAE introduisent des composants probabilistes, permettant de générer de nouvelles données similaires aux données d'entraînement.
Réseaux de Neurones de Mémoire à Long Terme (LSTM) :
- Utilisation Principale : Traitement du langage naturel, séquences temporelles.
- Caractéristiques : Les LSTMs sont une variation des RNN qui intègrent des mécanismes de portes pour mieux gérer le problème du gradient qui s'estompe sur de longues séquences. Ils sont couramment utilisés dans la génération de texte et d'autres tâches basées sur des séquences.

Feedforward neural network

Les réseaux de neurones en aval, également appelés réseaux de neurones à propagation avant (Feedforward Neural Networks), se caractérisent par une architecture où les connexions entre les nœuds ne forment pas de cycles. L'information se déplace de manière unidirectionnelle, des nœuds d'entrée vers les nœuds de sortie, sans boucles récurrentes.

Feedforward neural network

Pas de connexions cycliques : Contrairement aux réseaux récurrents, les réseaux de neurones en aval n'ont pas de connexions cycliques. Cela signifie qu'il n'y a pas de boucles ou de connexions récurrentes entre les couches, et l'information circule dans une seule direction.
Déplacement de l'information : L'information se déplace des nœuds d'entrée vers les nœuds de sortie en passant éventuellement par des nœuds cachés. Chaque couche de nœuds traite les données indépendamment, et les résultats sont transmis à la couche suivante.
Propagation avant (Forward Propagation) : La propagation avant est le processus par lequel les données sont transmises à travers le réseau, couche par couche, jusqu'à la couche de sortie. Chaque connexion entre les nœuds a un poids associé qui est ajusté pendant l'apprentissage.

Feedforward neural network

Apprentissage par rétropropagation (Backpropagation) : L'apprentissage dans les réseaux de neurones en aval se fait souvent par rétropropagation. Après la propagation avant, l'erreur entre la sortie prédite et la sortie réelle est calculée, puis cette erreur est rétropropagée à travers le réseau pour ajuster les poids et minimiser l'erreur.
Utilisation courante : Les réseaux de neurones en aval sont couramment utilisés pour des tâches telles que la classification, la régression, et d'autres problèmes où chaque exemple de données peut être traité de manière indépendante des autres.
Exemple d'application : Les réseaux de neurones en aval sont utilisés dans divers domaines tels que la vision par ordinateur, le traitement du langage naturel, la reconnaissance vocale, etc.

Rétropropagation du gradient (Backpropagation)

La rétropropagation du gradient, également appelée backpropagation, est une technique clé utilisée dans l'apprentissage des réseaux de neurones pour ajuster les poids des connexions afin de minimiser l'erreur globale du modèle.

Ajustement des poids pour compenser l'erreur : La rétropropagation ajuste les poids des connexions du réseau pour compenser chaque erreur constatée lors de l'apprentissage. L'objectif est de minimiser la différence entre les prédictions du modèle et les valeurs réelles de sortie.
Répartition de l'erreur entre les connexions : Le montant de l'erreur est réparti entre les connexions du réseau. Cela signifie que chaque poids contribue proportionnellement à l'erreur totale, et l'ajustement des poids est effectué en fonction de cette contribution.

Rétropropagation du gradient (Backpropagation)

Calcul du gradient de la fonction de perte : La rétropropagation calcule le gradient de la fonction de perte par rapport aux poids du réseau pour un seul exemple d'entrée-sortie. Le gradient représente la pente de la fonction de perte par rapport à chaque poids.
Règle de la chaîne : La rétropropagation fonctionne en utilisant la règle de la chaîne du calcul différentiel. Elle permet de décomposer la dérivée d'une fonction composée en une série de dérivées partielles. Dans le contexte de la rétropropagation, cela signifie calculer le gradient de la fonction de perte par rapport à chaque poids en remontant à travers le réseau.
Optimisation des poids par l'algorithme d'optimisation : Une fois que les gradients sont calculés, un algorithme d'optimisation, tel que la descente de gradient, est utilisé pour ajuster les poids dans la direction qui minimise la fonction de perte.

La rétropropagation est un processus itératif qui se déroule sur plusieurs cycles (itérations ou époques) d'entraînement du modèle. Elle contribue de manière significative à l'apprentissage des représentations et à l'amélioration des performances du réseau de neurones.

Rétropropagation du gradient (Backpropagation)

La rétropropagation du gradient implique le calcul des gradients de la fonction de perte par rapport aux poids du réseau. Pour expliquer le processus plus en détail, nous allons utiliser quelques notations courantes. Supposons que \(L\) soit la fonction de perte, \(w_{ij}^{(k)}\) soit le poids entre le neurone \(i\) dans la couche \(k-1\) et le neurone \(j\) dans la couche \(k\), et \(a_{i}^{(k)}\) soit l'activation du neurone \(i\) dans la couche \(k\).

Calcul de l'erreur : Supposons que \(y\) soit la sortie attendue et \(\hat{y}\) la sortie prédite. L'erreur pour un exemple donné est souvent mesurée par une fonction de perte, notée \(L\). \[ L = \text{fonction_de_perte}(y, \hat{y}) \]

Rétropropagation du gradient (Backpropagation)

Calcul du gradient de la fonction de perte par rapport à la sortie : \[ \frac{\partial L}{\partial \hat{y}} \]
Propagation arrière - règle de la chaîne : Pour chaque couche \(k\) en partant de la sortie jusqu'à l'entrée : \[ \delta_{i}^{(k)} = \frac{\partial L}{\partial a_{i}^{(k)}} \] \[ \frac{\partial L}{\partial w_{ij}^{(k)}} = a_{j}^{(k-1)} \cdot \delta_{i}^{(k)} \]

Rétropropagation du gradient (Backpropagation)

Mise à jour des poids avec un algorithme d'optimisation (e.g., descente de gradient) : \[ w_{ij}^{(k)} = w_{ij}^{(k)} - \eta \cdot \frac{\partial L}{\partial w_{ij}^{(k)}} \] \(\eta\) est le taux d'apprentissage.

Ces calculs sont effectués pour chaque exemple d'entraînement dans un lot (batch), et l'algorithme d'optimisation ajuste les poids pour minimiser la fonction de perte sur l'ensemble des données d'entraînement. Le processus est répété sur plusieurs époques jusqu'à ce que le modèle atteigne une performance souhaitée.

Réseau de neurones récurrents

Les réseaux de neurones récurrents (RNN) sont un type de réseau de neurones où les connexions entre les nœuds forment un graphe dirigé le long d'une séquence temporelle. Cela leur permet de présenter un comportement dynamique temporel, ce qui les rend particulièrement adaptés au traitement de séquences de données.

Connexions Temporelles : Les connexions entre les nœuds d'un RNN forment un graphe dirigé qui suit une séquence temporelle. Chaque nœud prend en compte l'entrée actuelle ainsi que l'état interne (mémoire) du réseau provenant de l'instant temporel précédent.
État Interne (Mémoire) : Les RNN utilisent leur état interne ou mémoire pour traiter des séquences d'entrées de longueur variable. Cela permet au réseau de mémoriser des informations importantes provenant des instants temporels précédents et de les utiliser pour influencer les prédictions actuelles.

Réseau de neurones récurrents

Les RNN sont largement utilisés dans des applications qui impliquent des données séquentielles, notamment :

Reconnaissance de l'écriture manuscrite : Les RNN peuvent être utilisés pour reconnaître des séquences de caractères dans une séquence d'écriture manuscrite.
Reconnaissance vocale : En traitant des séquences temporelles de signaux audio, les RNN peuvent être employés pour la reconnaissance vocale.

Réseau de neurones récurrents

Dans un réseau de neurones récurrents (RNN), le neurone, également appelé unité récurrente, est l'élément de base qui permet au réseau de traiter des données séquentielles en maintenant un état interne ou une mémoire.

Entrées : Le neurone RNN reçoit deux types d'entrées :

Entrée courante (\(x_t\)) : L'entrée actuelle à l'instant temporel \(t\). Elle peut représenter une caractéristique spécifique d'une séquence à cet instant.
État caché précédent (\(h_{t-1}\)) : L'état caché provenant de l'instant temporel précédent (\(t-1\)). Cet état représente la mémoire du réseau et est essentiel pour capturer les informations passées.

Réseau de neurones récurrents

Poids : Chaque connexion entre l'entrée courante, l'état caché précédent et le neurone a un poids associé (\(w\)). Ces poids déterminent l'importance respective des différentes entrées pour le neurone.
Fonction d'activation : Le neurone RNN utilise une fonction d'activation pour combiner les entrées et générer une sortie. La fonction d'activation est généralement non linéaire et permet au réseau d'apprendre des relations complexes dans les données séquentielles.
État caché (Mémoire) : La sortie du neurone à l'instant \(t\), souvent notée \(h_t\), devient l'état caché qui sera utilisé pour influencer la sortie à l'instant suivant (\(t+1\)). Cet état caché représente la mémoire du réseau et permet de conserver des informations importantes sur la séquence.

Réseau de neurones récurrents

Formule Générale : La sortie du neurone à l'instant \(t\) est calculée comme suit :

\[ h_t = \text{fonction_activation}(w_{hx} \cdot x_t + w_{hh} \cdot h_{t-1} + b_h) \] \(w_{hx}\) et \(w_{hh}\) sont les poids associés aux entrées actuelles et à l'état caché précédent, respectivement. \(b_h\) est le terme de biais.

Le rôle principal du neurone dans un RNN est de traiter séquentiellement les données en maintenant une mémoire du passé à travers l'état caché. Cette capacité à conserver des informations antérieures permet au RNN de modéliser des dépendances à long terme dans les séquences temporelles, ce qui est crucial pour des tâches telles que la reconnaissance de la parole, la traduction automatique, etc.

Réseau de neurones récurrents

Avantages

Traitement séquentiel : Les RNN sont spécialement conçus pour traiter des données séquentielles, ce qui en fait un choix naturel pour des tâches telles que la reconnaissance vocale, la traduction automatique et la prédiction temporelle.

Capacité à gérer les dépendances temporelles : Les RNN peuvent modéliser les dépendances à long terme dans les séquences temporelles en utilisant leur mémoire interne. Cela les rend adaptés à des problèmes où la compréhension du contexte temporel est essentielle.

Architecture réutilisable : La même architecture neuronale peut être utilisée à chaque instant temporel, facilitant ainsi la réutilisation des paramètres du modèle.

Flexibilité dans la taille des séquences : Les RNN peuvent traiter des séquences de longueurs variables, ce qui les rend adaptés à des données où la longueur de la séquence peut varier.

Réseau de neurones récurrents

Limites

Problème du gradient qui disparaît ou explose : L'entraînement de RNN sur de longues séquences peut entraîner des problèmes de gradients qui disparaissent ou explosent, ce qui rend l'apprentissage difficile.

Manque de captation de dépendances à très long terme : Malgré la capacité à gérer des dépendances à long terme, les RNN peuvent avoir du mal à capturer des dépendances très à long terme dans les séquences.

Calculs séquentiels : Les RNN effectuent des calculs de manière séquentielle, ce qui peut entraîner une lenteur dans le traitement par rapport à certaines architectures parallèles.

Sensibilité à l'ordre des éléments : Les RNN sont sensibles à l'ordre des éléments dans une séquence, et des permutations peuvent affecter le résultat du modèle.

Architectures améliorées nécessaires : Des architectures améliorées, telles que les LSTM (Long Short-Term Memory) et les GRU (Gated Recurrent Unit), sont souvent nécessaires pour atténuer les problèmes de gradient et améliorer la capacité du modèle à conserver des informations sur de longues séquences.

Réseau récurrent à mémoire court et long terme

Long short-term memory (LSTM) network

Les unités LSTM sont une variation de l'architecture des réseaux neuronaux récurrents (RNN) conçue pour résoudre le problème du gradient qui disparaît ou explose lors de l'entraînement de séquences à long terme. Elles sont particulièrement utiles pour modéliser les dépendances à long terme dans les séquences temporelles, telles que des séquences de mots dans le langage naturel.

Long short-term memory (LSTM) network

Connexions de retour d'information : Les connexions de retour d'information font référence à la capacité d'une unité LSTM à maintenir une mémoire à long terme en conservant des informations provenant d'itérations précédentes dans la séquence temporelle. Cette capacité à conserver des informations sur des intervalles de temps arbitraires est ce qui permet aux LSTM de gérer efficacement les dépendances à long terme dans les données séquentielles.
Cellule LSTM : La cellule LSTM est l'unité de mémoire principale. Elle stocke et régule l'information sur des intervalles de temps arbitraires. La cellule peut être considérée comme une mémoire à long terme qui peut être écrite, lue et modifiée.
Porte d'entrée (Input Gate): La porte d'entrée détermine quels éléments de la nouvelle information doivent être ajoutés à la cellule. Elle utilise une fonction d'activation pour contrôler cet ajout.

Long short-term memory (LSTM) network

Porte de sortie (Output Gate) : La porte de sortie décide quelle partie de l'information stockée dans la cellule doit être exposée à la sortie du LSTM. Elle utilise une fonction d'activation pour effectuer cette sélection.
Porte d'oubli (Forget Gate) : La porte d'oubli permet au LSTM de supprimer des informations de la cellule. Elle détermine quelles parties de l'information existante dans la cellule doivent être oubliées.

Ensemble, ces composants permettent à une unité LSTM de maintenir et de gérer des informations sur des périodes de temps étendues, ce qui en fait un choix puissant pour la modélisation de séquences temporelles complexes. Les portes d'entrée, de sortie et d'oubli fournissent un mécanisme de régulation fin pour contrôler le flux d'informations à travers la cellule.

Long short-term memory (LSTM) network

Supposons que \(x_t\) soit l'entrée à l'instant de temps \(t\), \(h_{t-1}\) soit la sortie de la couche LSTM à l'instant de temps précédent \(t-1\), et \(c_{t-1}\) soit l'état de la cellule à l'instant de temps précédent \(t-1\).

Porte d'entrée (Input Gate) :

\(i_t = \sigma(W_{ii} \cdot x_t + b_{ii} + W_{hi} \cdot h_{t-1} + b_{hi})\) (Activation)
\(\tilde{c}_t = \tanh(W_{ic} \cdot x_t + b_{ic} + W_{hc} \cdot h_{t-1} + b_{hc})\) (Nouvelles données de cellule proposées)
\(f_t = \sigma(W_{if} \cdot x_t + b_{if} + W_{hf} \cdot h_{t-1} + b_{hf})\) (Porte d'Oubli)

Long short-term memory (LSTM) network

Mise à jour de la cellule :

\(c_t = f_t \cdot c_{t-1} + i_t \cdot \tilde{c}_t\) (Mise à jour de l'état de la cellule)

Porte de sortie (Output Gate) :

\(o_t = \sigma(W_{io} \cdot x_t + b_{io} + W_{ho} \cdot h_{t-1} + b_{ho})\) (Activation)
\(h_t = o_t \cdot \tanh(c_t)\) (Sortie)

Long short-term memory (LSTM) network

Dans ces équations :

\(\sigma\) est la fonction sigmoïde.
\(\tanh\) est la fonction tangente hyperbolique.
\(W\) et \(b\) représentent les poids et les biais, respectivement, associés à différentes portes et entrées.
Les indices \(ii, ic, if, io\) indiquent les poids spécifiques pour les différentes portes.

Ces équations décrivent le flux d'information à travers une unité LSTM, avec des portes d'entrée, de sortie et d'oubli régulant l'interaction entre l'entrée, l'état de la cellule et la sortie. Ces formules permettent aux LSTM de maintenir et de gérer l'information sur des intervalles de temps arbitraires, ce qui les rend efficaces pour la modélisation de séquences temporelles complexes.

Réseaux de neurones convolutionnels

Source: https://en.wikipedia.org/wiki/File:Deep_Learning.jpg

Réseaux de neurones convolutionnels

Réseaux de neurones convolutionnels

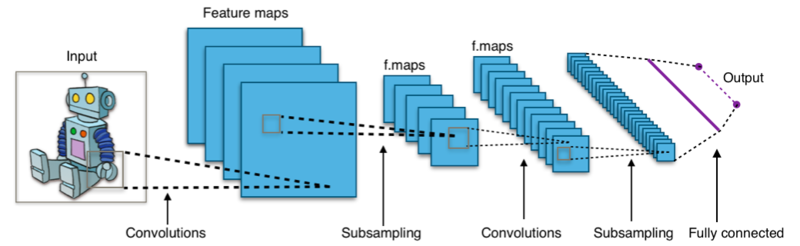
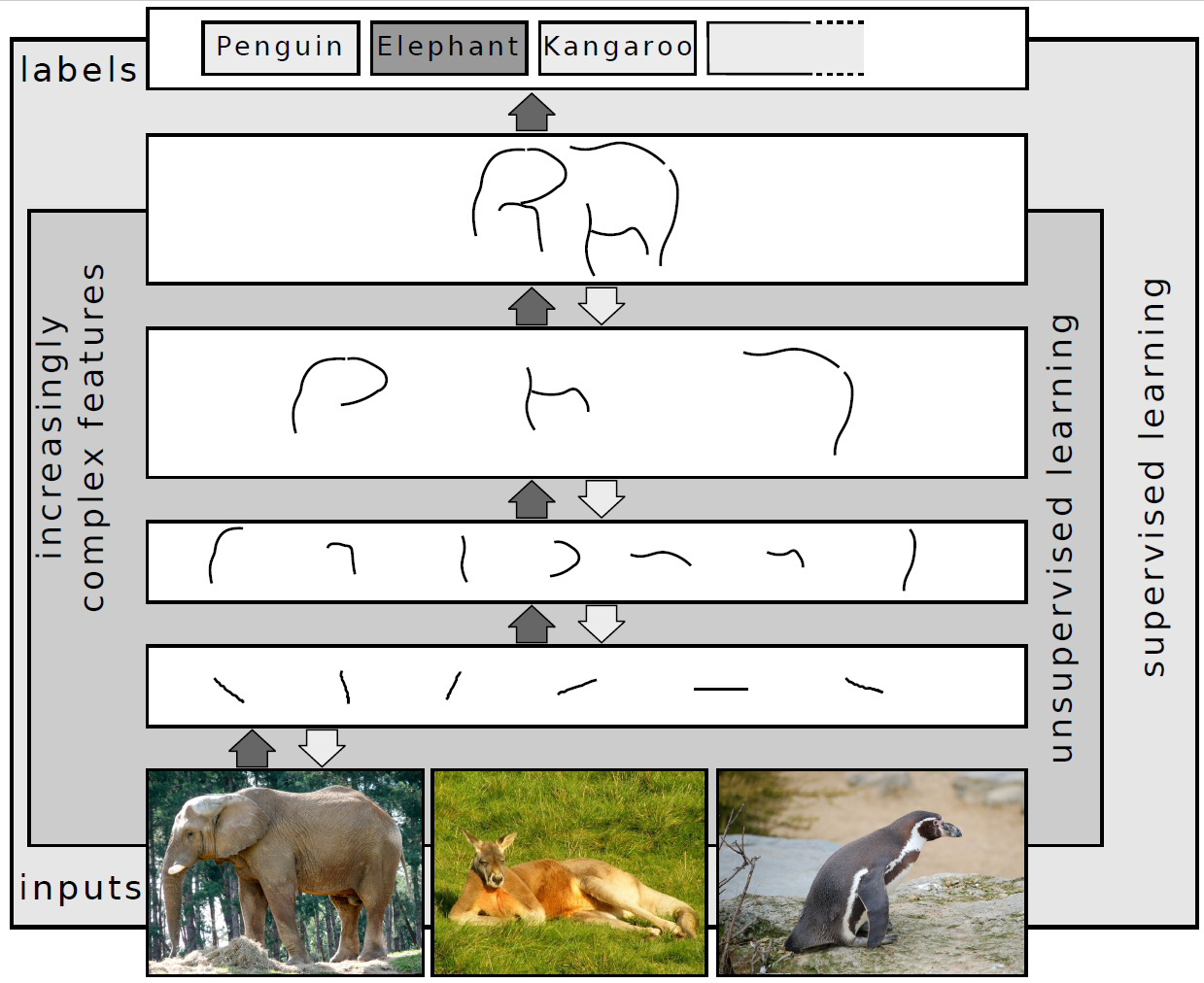
Les réseaux de neurones convolutionnels (CNN) sont une classe d'architectures de réseaux neuronaux conçues principalement pour l'analyse des images. Ils ont été particulièrement efficaces dans des tâches telles que la classification d'images, la détection d'objets, et la segmentation d'images.

Analyse des Images : Les CNN sont spécifiquement conçus pour travailler avec des données structurées en grilles, comme les images. Ils sont capables de capturer des motifs et des caractéristiques spatiales importantes dans les images.

Réseaux de neurones convolutionnels

Utilise la convolution La convolution est une opération mathématique linéaire utilisée pour extraire des caractéristiques locales à partir de l'image. Les filtres de convolution sont appliqués à l'image pour détecter des motifs tels que des bords, des textures, ou des formes.
Architecture en couches : Les CNN suivent généralement une architecture en couches. Ils ont une couche d'entrée pour recevoir l'image, une ou plusieurs couches cachées composées principalement de couches convolutives, et une couche de sortie pour produire les résultats finaux.

Réseaux de neurones convolutionnels

Couches convolutives : Les couches convolutives sont responsables de l'extraction des caractéristiques de l'image. Chaque couche peut avoir plusieurs filtres de convolution qui apprennent à détecter des motifs spécifiques. Ces couches sont souvent suivies de couches de pooling pour réduire la dimensionnalité de la représentation tout en préservant les caractéristiques importantes.
Applications : Les CNN sont largement utilisés dans des applications telles que la classification d'images (par exemple, reconnaître des animaux dans des photos), la détection d'objets (localiser et identifier des objets spécifiques), et la segmentation d'images (diviser une image en régions sémantiquement significatives)..

Réseaux de neurones convolutionnels: architecture

Modèle hiérarchique des données : Les réseaux neuronaux convolutifs (CNN) sont en effet conçus pour capturer des caractéristiques hiérarchiques dans les données, en particulier dans le contexte de l'analyse d'images. Cela signifie qu'ils peuvent apprendre des motifs simples dans les premières couches, puis combiner ces motifs pour former des caractéristiques plus complexes dans les couches suivantes.
Architecture d'un CNN : Un réseau neuronal convolutif est généralement composé d'une couche d'entrée, de plusieurs couches cachées et d'une couche de sortie. Les couches cachées consistent principalement en couches convolutionnelles, mais peuvent également inclure d'autres types de couches telles que des couches de regroupement (pooling), des couches entièrement connectées, et des couches de normalisation.

Réseaux de neurones convolutionnels: architecture

Couches convolutionnelles et fonction d'activation : Les couches convolutionnelles appliquent des filtres pour extraire des caractéristiques de l'image. La multiplication est effectuée par la convolution. La fonction d'activation la plus couramment utilisée est ReLU (Rectified Linear Unit), qui introduit une non-linéarité dans le modèle. Cette non-linéarité est importante pour permettre au réseau d'apprendre des relations complexes dans les données.
Couches supplémentaires : Après les couches de convolution, on peut avoir des couches de regroupement pour réduire la dimensionnalité, des couches entièrement connectées pour combiner des caractéristiques globales, et des couches de normalisation pour améliorer la stabilité de l'apprentissage.

En résumé, les CNN suivent une architecture hiérarchique, où les couches convolutives apprennent des caractéristiques locales, et ces caractéristiques sont ensuite combinées dans les couches suivantes pour former des représentations plus complexes. La non-linéarité introduite par la fonction d'activation ReLU est cruciale pour permettre au modèle d'apprendre des relations non linéaires dans les données.

Noyau (traitement d'image)

Un noyau dans le contexte du traitement d'images, également appelé filtre ou masque, est une petite matrice qui est appliquée sur une image à l'aide d'une opération de convolution. L'objectif de l'application de ces noyaux est de réaliser diverses opérations de filtrage sur l'image, telles que la détection de contours, l'amélioration des détails, la mise en évidence de certaines caractéristiques, etc.

Convolution dans les CNN : Dans les CNN, la convolution est une opération clé qui consiste à appliquer un ensemble de filtres (noyaux) à une image d'entrée. Chaque filtre est conçu pour extraire des caractéristiques spécifiques de l'image, comme des bords, des textures, ou d'autres motifs.

Noyau (traitement d'image)

Apprentissage des noyaux : L'une des caractéristiques importantes des CNN est la capacité d'apprendre les filtres (noyaux) de manière automatique pendant l'entraînement. Au lieu de définir manuellement les filtres comme dans le traitement d'images traditionnel, les CNN ajustent les poids des filtres pendant la phase d'apprentissage en fonction des caractéristiques qui sont importantes pour la tâche à accomplir.

Noyau (traitement d'image)

Rôle dans la hiérarchie des caractéristiques : Les premières couches d'un CNN apprennent généralement des filtres simples qui détectent des contours ou des textures de base. À mesure que l'on progresse dans les couches du réseau, les filtres deviennent plus complexes, capturant des caractéristiques de niveau supérieur, jusqu'à ce que la sortie finale représente des caractéristiques abstraites de l'image d'entrée.
Réduction de dimension avec le pooling : Après la convolution, les CNN utilisent souvent des couches de pooling pour réduire la dimension de la représentation, tout en préservant les caractéristiques importantes extraites par les filtres. Cela permet d'économiser des ressources computationnelles tout en maintenant les informations cruciales.

Noyau (traitement d'image)

Noyau d'identité

Il s'agit d'un noyau simple qui conserve l'image d'origine sans apporter de modifications. Lorsque ce noyau est appliqué à une image, il laisse l'image inchangée.

\( \begin{matrix} \ \ 0 &\ \ 0 &\ \ 0 \\ \ \ 0 &\ \ 1 &\ \ 0 \\ \ \ 0 &\ \ 0 &\ \ 0 \end{matrix} \)

Noyau (traitement d'image)

Noyau de détection de contours

Ce noyau est conçu pour détecter les contours dans une image. Il est également connu sous le nom de filtre de Sobel. Lorsqu'il est appliqué à une image, ce noyau met en évidence les variations d'intensité qui indiquent la présence de contours.

\( \begin{matrix} \ \ 1 & 0 & -1 \\ \ \ 0 & 0 & \ \ 0 \\ -1 & 0 & \ \ 1 \end{matrix} \)

Noyau (traitement d'image)

Box blur

Ce noyau est utilisé pour réaliser une opération de flou simple. Il est également connu sous le nom de flou moyen. Lorsqu'il est appliqué à une image, ce noyau attribue à chaque pixel la moyenne des valeurs de ses voisins, ce qui produit un effet de flou.

\( \frac{1}{9} \begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix} \)

Noyau (traitement d'image)

Flou de Gauss 3 × 3

Ce noyau est basé sur une distribution gaussienne et est utilisé pour réaliser un flou plus doux et plus esthétique. L'idée ici est que les pixels du centre ont un poids plus élevé, créant ainsi un effet de flou qui ressemble à celui généré par une lentille de caméra.

\( \frac{1}{16} \begin{matrix} 1 & 2 & 1 \\ 2 & 4 & 2 \\ 1 & 2 & 1 \end{matrix} \)

Convolution matricielle

La convolution est le processus central qui consiste à appliquer un noyau (aussi appelé filtre) sur une image. Cela se fait en déplaçant le noyau sur l'ensemble de l'image, multipliant les valeurs des pixels correspondants et produisant une nouvelle image appelée carte de caractéristiques.

\[ \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1n} \\ x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{mn} \\ \end{bmatrix} * \begin{bmatrix} y_{11} & y_{12} & \cdots & y_{1n} \\ y_{21} & y_{22} & \cdots & y_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ y_{m1} & y_{m2} & \cdots & y_{mn} \\ \end{bmatrix} = \sum^{m-1}_{i=0} \sum^{n-1}_{j=0} x_{(m-i)(n-j)} y_{(1+i)(1+j)} \]

Max pooling

Après la convolution, des opérations de pooling (souvent max pooling ou moyenne pooling) sont effectuées pour réduire la dimension de la carte de caractéristiques en préservant les informations importantes.

Stride et Padding

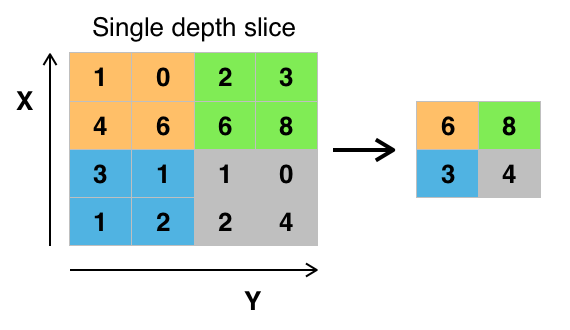
Stride : Contrôle le déplacement du noyau sur l'image. Un stride de 1 signifie un déplacement pixel par pixel, tandis qu'un stride plus grand réduit la taille de la carte de caractéristiques.

Padding : Ajoute des pixels autour de l'image d'entrée pour maintenir la taille de la sortie après la convolution.

Exemple: Tensorflow (réseaux de neurones convolutionnels)

            
import tensorflow as tf

from tensorflow.keras import datasets, layers, models

(train_images, train_labels), (test_images, test_labels) = datasets.cifar10.load_data()
train_images, test_images = train_images / 255.0, test_images / 255.0

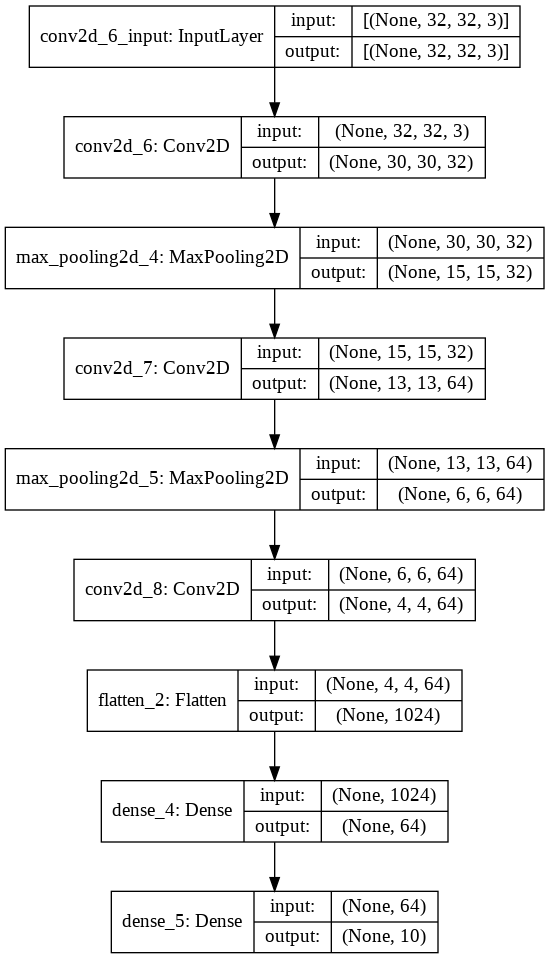
# Créer un modèle séquentiel (réseaux de neurones convolutionnels)
model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(32, 32, 3)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))

Exemple: Tensorflow (réseaux de neurones convolutionnels)

            
model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10)

#Compilation du modèle
model.compile(optimizer='adam',
   loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
   metrics=['accuracy'])

history = model.fit(train_images, train_labels, epochs=10,
   validation_data=(test_images, test_labels))

Exemple: Tensorflow (réseaux de neurones convolutionnels)

Modèle: https://www.tensorflow.org/tutorials/images/cnn

RCNN [Girshick 2014]

Les réseaux de neurones récurrents convolutifs (RCNN) sont une famille de modèles d'apprentissage automatique pour la vision par ordinateur, en particulier la détection d'objets. Ils combinent les avantages des réseaux de neurones récurrents (RNN) et des réseaux de neurones convolutifs (CNN).

Génération de propositions de régions : Une étape préliminaire consiste à générer un ensemble de propositions de régions, qui sont des régions de l'image qui pourraient contenir un objet. Cette étape est généralement effectuée en utilisant un algorithme bottom-up, tel que Selective Search.

RCNN [Girshick 2014]

Extraction de caractéristiques : Pour chaque proposition de région, un CNN est utilisé pour extraire des caractéristiques. Ces caractéristiques sont utilisées pour classifier la proposition de région en tant qu'objet ou non.
Classification : Enfin, un modèle de classification est utilisé pour classer chaque proposition de région en tant qu'objet ou non. Ce modèle peut être un classificateur SVM ou un classificateur à forêts aléatoires.

Bi-RCNN [Cai 2016,Wang 2020]

Bi-RCNN est une variante de RCNN qui utilise des réseaux de neurones récurrents bidirectionnels (Bi-RNN) pour améliorer la précision de la détection d'objets. Les Bi-RNN sont des modèles qui peuvent traiter des séquences de données dans les deux sens. Ils sont capables de capturer la dépendance entre les éléments d'une séquence, tant dans le passé que dans le futur. Dans le contexte de la détection d'objets, les Bi-RNN peuvent être utilisés pour capturer la relation entre les objets dans une image. Par exemple, un Bi-RNN peut être utilisé pour déterminer si deux objets sont proches l'un de l'autre, ou s'ils sont de la même classe.

Génération de propositions de régions : Une étape préliminaire consiste à générer un ensemble de propositions de régions, qui sont des régions de l'image qui pourraient contenir un objet. Cette étape est généralement effectuée en utilisant un algorithme bottom-up, tel que Selective Search.

Bi-RCNN [Cai 2016]

Extraction de caractéristiques : Pour chaque proposition de région, un CNN est utilisé pour extraire des caractéristiques. Ces caractéristiques sont ensuite transmises à un Bi-RNN.
Classification : Enfin, le Bi-RNN utilise les caractéristiques extraites pour classer la proposition de région en tant qu'objet ou non.

Bi-RCNN [Cai 2016]

Bi-RCNN est une méthode prometteuse pour améliorer la précision de la détection d'objets. Elle a été utilisée avec succès dans une variété de tâches, telles que la détection de personnes, la détection de véhicules et la détection de visages.

Détection de personnes : Bi-RCNN peut être utilisé pour capturer la relation entre les différentes parties du corps. Par exemple, Bi-RCNN peut être utilisé pour déterminer si les jambes d'une personne sont proches l'une de l'autre, ou si les bras d'une personne sont croisés.
Détection de véhicules : Bi-RCNN peut être utilisé pour capturer la relation entre les différents composants du véhicule. Par exemple, Bi-RCNN peut être utilisé pour déterminer si les phares d'une voiture sont allumés, ou si les roues d'une voiture sont tournantes.
Détection de visages : Bi-RCNN peut être utilisé pour capturer la relation entre les différents traits du visage. Par exemple, Bi-RCNN peut être utilisé pour déterminer si les yeux d'une personne sont ouverts, ou si la bouche d'une personne est souriante.

Articles de recherche

[Aly 2005] Aly, Mohamed. Survey on Multiclass Classification Methods. 2005.
[Cai 2016] Cai, Rui, et al. « Bidirectional Recurrent Convolutional Neural Network for Relation Classification ». Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), édité par Katrin Erk et Noah A. Smith, Association for Computational Linguistics, 2016, p. 756‑65. ACLWeb, https://doi.org/10.18653/v1/P16-1072.
[Girshick 2014] Girshick, Ross, et al. Rich feature hierarchies for accurate object detection and semantic segmentation. arXiv:1311.2524, arXiv, 22 octobre 2014. arXiv.org, https://doi.org/10.48550/arXiv.1311.2524.
[Jaakkola 2019] Jaakkola, H., et al. “Artificial Intelligence Yesterday, Today and Tomorrow.” 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2019, pp. 860–67. IEEE Xplore

Articles de recherche

[Krizhevsky 2012] Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Advances in neural information processing systems. 2012;25.
[Pan 2016] Pan, Yunhe, “Heading toward Artificial Intelligence 2.0.” Engineering, vol. 2, no. 4, Dec. 2016, pp. 409–13. www.sciencedirect.com,
[Simonyani 2015] Simonyani K., Zisserman A., Very Deep Convolutional Networks for Large-Scale Image Recognition. International Conference on Learning Representations, 2015
[Wang 2020] Wang, Hongbo, et al. « A Comprehensive Overview of Person Re-Identification Approaches ». IEEE Access, vol. 8, 2020, p. 45556‑83. IEEE Xplore, https://doi.org/10.1109/ACCESS.2020.2978344.

Web

Réglage des hyperparamètres avec le tableau de bord HParams https://www.tensorflow.org/tensorboard/hyperparameter_tuning_with_hparams?hl=fr

Couleurs

Color Tool - Material Design

Images

Wikimedia Commons

Intelligence artificielle et Deep Learning

Apprentissage profond

3.1. Apprentissage profond: introduction

Perceptron simple couche

3.1. Apprentissage profond: introduction

Perceptron simple couche

3.1. Apprentissage profond: introduction

Perceptron simple couche

3.1. Apprentissage profond: introduction

Perceptron multicouche

3.1. Apprentissage profond: introduction

Perceptron multicouche

3.1. Apprentissage profond: introduction

Perceptron multicouche

3.1. Apprentissage profond: introduction

Réseau de Neurones Profond

3.1. Apprentissage profond: introduction

Exemple: Tensorflow

3.1. Apprentissage profond: introduction

Exemple: Tensorflow

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

3.1. Apprentissage profond: introduction

Composants des réseaux de neurones artificiels

Organisation

3.1. Apprentissage profond: introduction

Composants des réseaux de neurones artificiels

Organisation

3.1. Apprentissage profond: introduction

Composants des réseaux de neurones artificiels

Organisation et connectivité

3.1. Apprentissage profond: introduction

Composants des réseaux de neurones artificiels

Organisation et connectivité

3.1. Apprentissage profond: introduction

Composants des réseaux de neurones artificiels

Organisation et connectivité

3.1. Apprentissage profond: introduction

Composants des réseaux de neurones artificiels

Organisation et connectivité

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones profonds

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones profonds

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones profonds

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

Fonctions d'activation pour les réseaux de neurones convolutifs (CNN)

3.1. Apprentissage profond: introduction

Réseaux de neurones artificiels: Hyperparamètres

Fonctions de perte