Intelligence artificielle et Deep Learning
Apprentissage machine
John Samuel
CPE Lyon
Année: 2024-2025
Courriel: john.samuel@cpe.fr


| Aspect | Neurone Biologique | Neurone Artificiel |
|---|---|---|
| Structure | Composé de dendrites, d’un soma (corps cellulaire), et d’un axone | Composé de poids (équivalents aux connexions), biais, et activation |
| Fonction | Transmet des impulsions électriques entre les neurones | Calcule une valeur de sortie en fonction de la somme pondérée des entrées |
| Entrée | Reçoit des signaux par les dendrites | Reçoit des valeurs pondérées (par les poids) |
| Poids des connexions | La force des synapses influence l’intensité du signal transmis | Les poids déterminent l’importance de chaque entrée |
| Aspect | Neurone Biologique | Neurone Artificiel |
|---|---|---|
| Activation | Un potentiel d’action est déclenché si le signal dépasse un seuil | Une fonction d’activation est appliquée pour déterminer la sortie |
| Sortie | Envoie un signal via l’axone vers d’autres neurones | Produit une sortie, souvent transmise aux neurones suivants dans le réseau |
| Apprentissage | Renforce les connexions synaptiques en fonction de l’expérience (plasticité synaptique) | Ajuste les poids via des algorithmes d’apprentissage (ex. rétropropagation) |
| Rôle | Participe à des processus cognitifs complexes | Contribue aux calculs et à la reconnaissance de motifs |
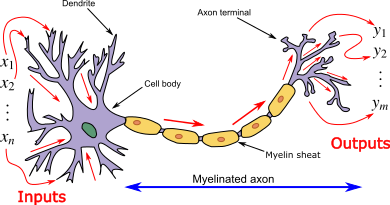
Les réseaux de neurones sont couramment utilisés dans le domaine de l'apprentissage machine, en particulier dans des tâches telles que la classification, la régression, la reconnaissance d'images, le traitement du langage naturel, et bien d'autres. Un réseau de neurones artificiels est une collection d'unités interconnectées appelées neurones artificiels. Ces réseaux sont inspirés de la structure du cerveau biologique
Le perceptron est un algorithme d'apprentissage supervisé utilisé pour la classification binaire. Il est conçu pour résoudre des problèmes où l'objectif est de déterminer si une entrée donnée appartient ou non à une classe particulière.

Le perceptron utilise généralement une fonction d'activation simple, et la fonction d'échelon (step function) est fréquemment choisie pour cette tâche.
La fonction d'échelon attribue une sortie de 1 si la somme pondérée des entrées dépasse un certain seuil, et 0 sinon.
\( f(x) = \begin{cases} 1 & \text{si } x \geq \text{seuil} \\ 0 & \text{sinon} \end{cases} \)
import numpy as np
class Perceptron:
def __init__(self, taux_apprentissage=0.01, n_iterations=1000):
self.taux_apprentissage = taux_apprentissage
self.n_iterations = n_iterations
self.poids = None
self.biais = None
class Perceptron:
def ajuster(self, X, y):
n_exemples, n_caracteristiques = X.shape
self.poids = np.zeros(n_caracteristiques)
self.biais = 0
for _ in range(self.n_iterations):
for i in range(n_exemples):
ligne = X[i]
y_calculé = np.dot(ligne, self.poids) + self.biais
prediction = 1 if y_calculé >= 0 else 0
erreur = y[i] - prediction
# Mise à jour des poids et biais
self.poids += self.taux_apprentissage * erreur * ligne
self.biais += self.taux_apprentissage * erreur
class Perceptron:
def predire(self, X):
y_calculé = np.dot(X, self.poids) + self.biais
return np.where(y_calculé >= 0, 1, 0)
# Données d'exemple
X = np.array([[1, 1], [2, 2], [1.5, 1.5], [0, 0], [0.5, 0.5], [1, 0]])
y = np.array([1, 1, 1, 0, 0, 0])
# Création et entraînement du perceptron
perceptron = Perceptron(taux_apprentissage=0.1, n_iterations=10)
perceptron.ajuster(X, y)
# Prédiction
print(perceptron.predire(np.array([[1, 1], [0, 0]]))) # Sortie : [1 0]
Un MLP est composé de plusieurs couches de neurones. Chaque neurone dans une couche est connecté à tous les neurones de la couche suivante (d’où le nom de “réseau de neurones entièrement connecté”). Un MLP possède typiquement
Les poids \( W \) et les biais \( b \) sont initialisés aléatoirement pour chaque connexion entre les neurones. Par exemple, pour une couche \( l \) de \( n_l \) neurones connectée à la couche \( l+1 \) de \( n_{l+1} \) neurones :
import numpy as np
# Initialisation de la structure du réseau
couches = [3, 5, 4, 1] # exemple : 3 neurones d'entrée, 2 couches cachées de 5 et 4 neurones, et 1 neurone de sortie
# Initialisation des poids et biais aléatoires
poids = [np.random.rand(couches[i], couches[i + 1]) for i in range(len(couches) - 1)]
biais = [np.random.rand(1, couches[i + 1]) for i in range(len(couches) - 1)]
La propagation avant consiste à faire passer les données d’entrée à travers chaque couche du réseau. À chaque neurone, on effectue une combinaison linéaire de ses entrées (poids * entrée + biais) suivie d’une fonction d’activation.
Les fonctions d’activation courantes sont : -
La propagation avant est le processus par lequel les données d’entrée traversent les couches du réseau. À chaque neurone de la couche \( l \), on calcule une activation basée sur une combinaison linéaire des activations de la couche précédente, suivie d’une fonction d’activation.
Soit \( a^{(l)} \) l’activation de la couche \( l \) :
# Fonction d'activation Sigmoïde
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Fonction d'activation ReLU
def relu(x):
return np.maximum(0, x)
# Propagation avant à travers le réseau
def propagation_avant(entree, poids, biais):
activation = entree
activations = [activation] # stocke les activations de chaque couche pour le backprop
# Propagation à travers chaque couche cachée
for i in range(len(poids) - 1):
z = np.dot(activation, poids[i]) + biais[i]
activation = relu(z) # on utilise ReLU pour les couches cachées
activations.append(activation)
# Couche de sortie (par ex., sigmoid pour une tâche de classification binaire)
z = np.dot(activation, poids[-1]) + biais[-1]
activation = sigmoid(z)
activations.append(activation)
return activations
Une fois les prédictions faites, il est essentiel de calculer l’erreur. Dans le cas de la classification binaire, la log-loss ou l’entropie croisée binaire est couramment utilisée. Cette étape permet de quantifier l’écart entre les prédictions et les vraies étiquettes.
Pour évaluer la qualité des prédictions, on utilise une fonction de perte. Dans le cas d’une tâche de classification binaire, la log-loss (ou entropie croisée binaire) est souvent utilisée.
Si \( y \) est la véritable étiquette et \( \hat{y} \) la prédiction, la perte pour un exemple est donnée par : \[ \text{Perte} = - \left( y \cdot \log(\hat{y}) + (1 - y) \cdot \log(1 - \hat{y}) \right) \]
Pour un ensemble de \( m \) exemples, la perte totale devient : \[ \text{J}(W, b) = -\frac{1}{m} \sum_{i=1}^{m} \left( y^{(i)} \cdot \log(\hat{y}^{(i)}) + (1 - y^{(i)}) \cdot \log(1 - \hat{y}^{(i)}) \right) \]
# Fonction de perte (Binary Cross-Entropy)
def calcul_perte(y_pred, y_vrai):
m = y_vrai.shape[0]
perte = -np.sum(y_vrai * np.log(y_pred) + (1 - y_vrai) * np.log(1 - y_pred)) / m
return perte
La rétropropagation ajuste les poids et les biais en fonction de l’erreur obtenue. Elle utilise le gradient de la perte pour chaque paramètre du réseau, appliqué depuis la couche de sortie jusqu’à la couche d’entrée.
La rétropropagation est utilisée pour calculer le gradient de la perte par rapport aux paramètres \( W \) et \( b \), et ajuster ces paramètres pour réduire l’erreur.
Les poids et les biais sont ajustés à chaque itération pour minimiser la perte en utilisant le **gradient descend** avec un taux d’apprentissage \( \alpha \) :
\[ W^{(l)} := W^{(l)} - \alpha \frac{\partial J}{\partial W^{(l)}} \]
\[ b^{(l)} := b^{(l)} - \alpha \frac{\partial J}{\partial b^{(l)}} \]
# Fonction de dérivée pour Sigmoïde et ReLU
def derivee_sigmoid(x):
return x * (1 - x)
def derivee_relu(x):
return np.where(x > 0, 1, 0)
# Rétropropagation
def retropropagation(activations, poids, biais, y_vrai, taux_apprentissage=0.01):
# Étape 1 : Calculer le gradient de la perte pour la couche de sortie
erreur = activations[-1] - y_vrai
deltas = [erreur * derivee_sigmoid(activations[-1])]
# Étape 2 : Calculer les gradients pour chaque couche cachée
for i in reversed(range(len(poids) - 1)):
delta = np.dot(deltas[-1], poids[i + 1].T) * derivee_relu(activations[i + 1])
deltas.append(delta)
# Inverser les deltas pour qu'ils correspondent à chaque couche du réseau
deltas = deltas[::-1]
# Mise à jour des poids et biais
for i in range(len(poids)):
poids[i] -= taux_apprentissage * np.dot(activations[i].T, deltas[i])
biais[i] -= taux_apprentissage * np.sum(deltas[i], axis=0, keepdims=True)
L’entraînement du réseau consiste à itérer sur les étapes de propagation avant, de calcul de l’erreur, et de rétropropagation plusieurs fois (époques) pour ajuster les paramètres et minimiser l’erreur.
def entrainer_mlp(X, y, couches, epochs=1000, taux_apprentissage=0.01):
# Initialisation des poids et biais
poids = [np.random.rand(couches[i], couches[i + 1]) for i in range(len(couches) - 1)]
biais = [np.random.rand(1, couches[i + 1]) for i in range(len(couches) - 1)]
# Boucle d'entraînement
for epoch in range(epochs):
# Propagation avant
activations = propagation_avant(X, poids, biais)
# Calcul de la perte
perte = calcul_perte(activations[-1], y)
# Rétropropagation
retropropagation(activations, poids, biais, y, taux_apprentissage)
# Afficher la perte à intervalles réguliers
if epoch % 100 == 0:
print(f"Epoch {epoch}, Perte: {perte:.4f}")
return poids, biais
Après l’entraînement, le modèle peut être utilisé pour faire des prédictions sur de nouvelles données en effectuant simplement une propagation avant.
Pour effectuer une prédiction après l'entraînement, on utilise simplement la propagation avant. La sortie de la couche finale \( a^{(L)} \) est interprétée en fonction de la tâche :
Pour la classification binaire, on utilise une règle de décision, par exemple : \[ \hat{y} = \begin{cases} 1 & \text{si } a^{(L)} \geq 0.5 \\ 0 & \text{sinon} \end{cases} \]
# Fonction de prédiction
def predire(X, poids, biais):
activations = propagation_avant(X, poids, biais)
return activations[-1]
Les neurones sont organisés en couches. Il existe généralement trois types de couches dans un réseau de neurones :
L'objectif global de l'entraînement est d'ajuster les poids du réseau de manière à ce qu'il puisse généraliser à de nouvelles données, produisant des résultats précis pour des exemples qu'il n'a pas vu pendant l'entraînement.
Chaque neurone artificiel a des entrées, qui peuvent être les valeurs caractéristiques d'un échantillon de données externe, et produit une seule sortie. Cette sortie peut être envoyée à plusieurs autres neurones, formant ainsi la structure interconnectée du réseau neuronal. La fonction d'activation joue un rôle crucial dans le calcul de la sortie d'un neurone. Le processus comprend les étapes suivantes :
Le réseau de neurones est constitué de connexions, où chaque connexion transmet la sortie d'un neurone comme entrée à un autre neurone. Chaque connexion possède un poids qui représente son importance relative dans la transmission du signal.
Calcul de l'entrée d'un neurone : La fonction de propagation calcule l'entrée d'un neurone en prenant la somme pondérée des sorties de ses prédécesseurs, où chaque sortie est multipliée par le poids de la connexion correspondante. Cela peut être représenté mathématiquement comme suit :
\[ \text{Entrée du Neurone} = \sum_{i=1}^{n} (\text{Sortie du Prédécesseur}_i \times \text{Poids}_i) \] où \(n\) est le nombre de connexions d'entrée.
Ajout d'un terme de biais : Un terme de biais peut être ajouté au résultat de la propagation. Le terme de biais est un paramètre supplémentaire, souvent représenté par \(b\) dans les équations, qui permet au modèle d'apprendre un décalage ou une translation. Cela donne la forme finale de l'entrée du neurone :
\[ \text{Entrée du Neurone} = \sum_{i=1}^{n} (\text{Sortie du Prédécesseur}_i \times \text{Poids}_i) + \text{Biais} \]
Fonction d'Activation : Après avoir calculé l'entrée du neurone, celle-ci est passée à travers une fonction d'activation. Cette fonction introduit une non-linéarité dans le modèle, permettant au réseau de neurones de capturer des relations complexes et d'apprendre des modèles non linéaires. Certaines des fonctions d'activation couramment utilisées comprennent :
\[f(x)=x\]
\[f'(x)=1\]
\[f(x) = \begin{cases} 0 & \text{for } x < 0\\ 1 & \text{for } x \ge 0 \end{cases} \]
\[f'(x) = \begin{cases} 0 & \text{for } x \ne 0\\ ? & \text{for } x = 0\end{cases}\]
\[f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\]
\[f'(x)=f(x)(1-f(x))\]
\[f(x)=\tanh(x)=\frac{(e^{x} - e^{-x})}{(e^{x} + e^{-x})}\]
\[f'(x)=1-f(x)^2\]
\[f(x) = \begin{cases} 0 & \text{for } x \le 0\\ x & \text{for } x > 0\end{cases} = \max\{0,x\}= x \textbf{1}_{x>0}\]
\[f'(x) = \begin{cases} 0 & \text{for } x \le 0\\ 1 & \text{for } x > 0\end{cases}\]
\[f(x)=e^{-x^2}\]
\[f'(x)=-2xe^{-x^2}\]