Traitement de données massives

John Samuel
CPE Lyon

Year: 2023-2024
Email: john.samuel@cpe.fr

Objectifs

1. Régularités
2. Exploration des données
3. Algorithmes
4. Sélection de caractéristiques

Régularités naturelles

• Symétrie
• Arbres, fractales
• Spirales
• Chaos
• Ondes
• Bulles, mousse
• Pavages
• Ruptures
• Taches, bandes

Créations humaines

• Bâtiments (Symétrie) : Structures construites par l'homme avec des motifs de symétrie. Exemple : Cathédrales gothiques, gratte-ciels modernes.
• Villes : Agglomérations planifiées ou organiques habitées par les humains. Exemple : Paris, New York.
• Environnement virtuel (e.g., jeux de vidéo) : Espaces créés numériquement pour l'interaction humaine. Exemple : Mondes ouverts dans les jeux vidéo, simulations virtuelles.
• Les artefacts humains : Objets fabriqués par les humains dans divers domaines. Exemple : Outils préhistoriques, œuvres d'art contemporaines.

Création

• Répétition
• Fractales : Structures mathématiques auto-similaires à différentes échelles.
  • Ensemble de Julia: Un ensemble fractal défini par une fonction itérative f(z) = z² + c
  • Caractéristiques : produit des motifs répétitifs complexes lorsqu'il est visualisé.

Synonymes

• Fouille de données
• Forage de données
• Extraction de connaissances à partir de données
• Data mining
• Machine learning
• Apprentissage automatique

Approches

• Apprentissage supervisé : Le modèle est entraîné sur un ensemble de données étiquetées où les exemples d'entrée sont associés à des sorties désirées. Le modèle apprend à faire des prédictions sur de nouvelles données en se basant sur ces associations.
• Apprentissage non supervisé : Le modèle est exposé à des données non étiquetées et cherche à découvrir des modèles, des structures ou des relations intrinsèques dans les données.
• Apprentissage semi-supervisé : Une combinaison des deux précédents, utilisant à la fois des données étiquetées et non étiquetées pour l'entraînement.
• Apprentissage par renforcement : Le modèle apprend à prendre des décisions en interagissant avec son environnement. Il reçoit des récompenses ou des pénalités en fonction de ses actions, ce qui guide son apprentissage.

Formalisation

• Vecteur euclidien:
  • Un vecteur euclidien est un objet géométrique caractérisé par sa magnitude (longueur) et sa direction.
  • Les vecteurs euclidiens sont couramment utilisés pour représenter des données sous forme de points dans un espace multidimensionnel, où chaque dimension correspond à une caractéristique ou une variable.
• Espace vectoriel:
  • Un espace vectoriel est une collection de vecteurs qui peuvent être additionnés entre eux et multipliés par des nombres (scalaires).

Formalisation

• Vecteur de caractéristiques (features):
  • Un vecteur de caractéristiques est un vecteur n-dimensionnel qui représente les caractéristiques ou les attributs d'une entité.
• Espace de caractéristiques:
  • L'espace de caractéristiques est l'espace vectoriel associé aux vecteurs de caractéristiques.
  • Chaque dimension de cet espace représente une caractéristique particulière, et les vecteurs sont utilisés pour positionner les données dans cet espace en fonction de leurs caractéristiques.

Exemples de caractéristiques

• Images: Dans le contexte des images, les vecteurs de caractéristiques peuvent être construits à partir des valeurs des pixels. Chaque pixel peut être considéré comme une dimension, et un vecteur de caractéristiques contiendra les valeurs de tous les pixels, permettant ainsi de représenter une image sous forme de vecteur.
• Textes: Pour les textes, les vecteurs de caractéristiques sont souvent construits à partir de la fréquence d'apparition des mots, des phrases, ou des tokens dans un document. Cela permet de représenter le contenu textuel en utilisant des valeurs numériques, ce qui est essentiel pour l'analyse de texte et la recherche d'informations.

Formalisation

• Construction de caractéristiques¹:
  • La construction de caractéristiques consiste à créer de nouvelles variables ou attributs à partir de celles déjà présentes dans les données.
  • Cette étape peut être cruciale pour améliorer les performances des modèles d'apprentissage machine en introduisant des informations pertinentes et en éliminant du bruit.
• Opérateurs de construction pour les caractéristiques
  • Les opérateurs de construction sont des fonctions ou des opérations mathématiques qui permettent de créer de nouvelles caractéristiques à partir de celles existantes.
  • Parmi les opérateurs couramment utilisés, on trouve les opérateurs d'égalité (comparaisons), les opérateurs arithmétiques (addition, soustraction, multiplication, division), les opérateurs de tableau (min, max, moyenne, médiane, etc.), les fonctions de transformation, etc.

1. https://en.wikipedia.org/wiki/Feature_vector

Exemple

• Soit Année de naissance et Année de décès deux caractéristiques existantes.
• Une nouvelle caractéristique appelée âge est créée. âge = Année de décès - Année de naissance

La construction de caractéristiques est une étape essentielle dans le pipeline de prétraitement des données en apprentissage machine, car elle peut aider à rendre les données plus informatives pour les algorithmes d'apprentissage.

Formalisation: Apprentissage supervisé

• Le nombre d'exemples d'entraînement (N) : Cela représente la quantité d'exemples de données que vous avez pour entraîner un modèle supervisé. Chaque exemple d'entraînement se compose d'un vecteur de caractéristiques (x) et de son label (y).
• L'espace de saisie des caractéristiques (X) : C'est l'ensemble de toutes les combinaisons possibles de vecteurs de caractéristiques qui peuvent être utilisées comme entrée pour le modèle. Cet espace est défini par les caractéristiques que vous avez extraites des données.
• L'espace des caractéristiques de sortie (Y) : Il représente l'ensemble de toutes les valeurs possibles que peuvent prendre les étiquettes ou les labels.
• Exemples d'entraînement (D) : C'est votre ensemble de données d'entraînement, composé de paires (x, y) où x est le vecteur de caractéristiques et y est le label correspondant.

Formalisation: Apprentissage supervisé

• Objectif de l'algorithme d'apprentissage supervisé : Il s'agit de trouver une fonction (g) qui associe un vecteur de caractéristiques (x) à un label (y). L'ensemble des fonctions possibles est appelé espace des hypothèses (G). L'objectif est de choisir la fonction (g) qui minimise l'erreur de prédiction sur les exemples d'entraînement et généralise bien sur de nouvelles données.
• Fonction d'évaluation (F) : Elle indique l'espace des fonctions d'évaluation utilisées pour évaluer la performance des fonctions hypothétiques. L'objectif est de trouver la fonction (g) qui renvoie la fonction d'évaluation (f) la plus élevée, c'est-à-dire celle qui donne les prédictions les plus précises.

Formalisation: Apprentissage supervisé

Cette formalisation est au cœur de l'apprentissage supervisé, où l'objectif est d'apprendre à partir d'exemples étiquetés et de trouver une fonction qui puisse prédire de manière précise les étiquettes pour de nouvelles données non vues.

• Soit \(N\) le nombre d'exemples d'entraînement
• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• Soit \({(x_1, y_1),...,(x_N, y_N)}\) les \(N\) exemples d'entraînement, où
  • \(x_i\) est le vecteur de caractéristiques de i^ème exemple d'entraînement.
  • \(y_i\) est son label.

Formalisation: Apprentissage supervisé

• L'objectif de l'algorithme d'apprentissage supervisé est de trouver \(g: X → Y\), où
  • g est l'une des fonctions de l'ensemble des fonctions possibles G (espace des hypothèses)
• Fonction d'évaluation F indiquent l'espace des fonctions d'évaluation, où
  • \(f: X × Y → R\) telle que g renvoie la fonction d'évaluation la plus élevée.

Formalisation: Apprentissage non supervisé

• L'espace de saisie des caractéristiques (X) : C'est l'ensemble de toutes les combinaisons possibles de vecteurs de caractéristiques qui peuvent être utilisées comme entrée pour le modèle en apprentissage non supervisé. Cet espace est défini par les caractéristiques que vous avez extraites des données.
• L'espace des caractéristiques de sortie (Y) : Il représente l'ensemble des caractéristiques de sortie potentielles. Contrairement à l'apprentissage supervisé, en apprentissage non supervisé, Y ne consiste pas en des étiquettes ou des labels prédéfinis, mais plutôt en des transformations, des représentations, ou des caractéristiques extraites des données d'entrée.

Formalisation: Apprentissage non supervisé

• Objectif de l'algorithme d'apprentissage non supervisé : L'objectif est de trouver une correspondance entre l'espace de saisie des caractéristiques (X) et l'espace des caractéristiques de sortie (Y). Cela peut impliquer diverses tâches, telles que la réduction de la dimensionnalité, la classification automatique de données non étiquetées, la détection d'anomalies, la segmentation, ou la représentation latente des données.
• Mise en correspondance X → Y : Cette mise en correspondance peut être réalisée de différentes manières, selon la tâche d'apprentissage non supervisé spécifique. Par exemple, dans la réduction de la dimensionnalité, X peut être une représentation à haute dimension des données, tandis que Y représente la version réduite de ces données, souvent avec moins de dimensions.

Formalisation: Apprentissage non supervisé

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• L'objectif de l'algorithme d'apprentissage non supervisé est
  • trouver la mise en correspondance \(X → Y\)

L'apprentissage non supervisé est utilisé pour explorer et découvrir des modèles, des structures ou des caractéristiques inhérentes aux données, sans l'utilisation d'étiquettes ou de labels préalables. Il est couramment utilisé dans des domaines tels que la clustering, l'analyse de composantes principales (PCA), l'analyse en composantes indépendantes (ICA), et bien d'autres.

Formalisation: Apprentissage semi-supervisé

• L'espace de saisie des caractéristiques (X) : Il s'agit de l'ensemble de toutes les combinaisons possibles de vecteurs de caractéristiques qui peuvent être utilisés comme entrée pour le modèle en apprentissage semi-supervisé.
• L'espace des caractéristiques de sortie (Y) : Il représente l'ensemble des caractéristiques de sortie potentielles, mais contrairement à l'apprentissage supervisé, il n'est pas nécessairement constitué d'étiquettes ou de labels prédéfinis.
• Ensemble d'exemples d'exercices étiquetés (l) : Cela correspond à un sous-ensemble d'exemples qui ont été annotés ou étiquetés avec des valeurs de sortie connues.
• Ensembles des vecteurs de caractéristiques non étiquetées (u) : Il s'agit des exemples non étiquetés, où les valeurs de sortie ne sont pas connues.

Formalisation: Apprentissage semi-supervisé

• Objectif de l'algorithme d'apprentissage semi-supervisé : L'objectif principal est de trouver des étiquettes correctes pour les exemples non étiquetés (apprentissage transductif), ainsi que de trouver la bonne mise en correspondance entre les caractéristiques d'entrée et les caractéristiques de sortie (apprentissage inductif).
  • Apprentissage transductif : Il s'agit de trouver des étiquettes correctes pour les exemples non étiquetés. Cela revient à prédire les valeurs de sortie pour les exemples non étiquetés sans nécessairement chercher à généraliser à de nouvelles données.
  • Apprentissage inductif : Cela concerne la recherche de la bonne mise en correspondance entre les vecteurs de caractéristiques d'entrée et les caractéristiques de sortie. Cela peut inclure la généralisation à de nouvelles données en utilisant le modèle appris.

Formalisation: Apprentissage semi-supervisé

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• Soit \({(x_1, y_1),...,(x_l, y_l)}\) l'ensemble d'exemples d'exercices étiquetés
• Soit \({x_{l+1},...,x_{l+u}}\) sont les \(u\) ensembles des vecteurs de caractéristiques non étiquetées de \(X\).
• L'objectif de l'algorithme d'apprentissage semi-supervisé est de faire
  • l'apprentissage transductif, c'est-à-dire trouver des étiquettes correctes pour \({x_{l+1},...,x_{l+u}}\).
  • l'apprentissage inductif, c'est-à-dire trouver la bonne mise en correspondance \(X → Y\)

Activités

1. Classification
2. Partitionnement de données (Clustering)
3. Régression
4. Étiquetage des séquences
5. Règles d'association
6. Détection d'anomalies
7. Récapitulation

2.1.1 Introduction

• Catégorisation algorithmique d'objets : Processus d'attribution de classes ou de catégories à des objets via des algorithmes. L'objectif est d'organiser les données en groupes distincts pour faciliter l'analyse et la prise de décision.
• Attribution de classes :Attribuer une classe ou catégorie à chaque objet (ou individu).
• Types de classification :
  • Classification binaire : Assignation à deux classes.
  • Classification en classes multiples : Assignation à plusieurs classes simultanément.

Applications

• Filtrage de contenu (e.g., spam/pourriel) : Identifier et filtrer les emails non désirés ou indésirables. Exemple : Filtrage des spams dans les boîtes de réception.
• Classification de documents : Organiser et catégoriser les documents en fonction de leur contenu. Exemple : Classification automatique des articles de presse par sujet.
• Reconnaissance de l'écriture manuscrite : Interprétation automatique des caractères écrits à la main. Exemple : Reconnaissance des chiffres sur les chèques bancaires.
• Reconnaissance automatique de la parole : Convertir la parole en texte écrit de manière automatique. Exemple : Commandes vocales pour les assistants virtuels comme Siri ou Alexa.
• Moteurs de recherche : Classer et organiser les résultats de recherche en fonction de leur pertinence. Exemple : Classement des pages web dans les résultats de recherche de moteurs de recherche.

Classification: Définition formelle

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• L'objectif de l'algorithme de classification (ou classificateur) est de trouver \({(x_1, y_1),...,(x_l, y_k)}\), c'est-à-dire l'attribution d'une étiquette connue à chaque vecteur de caractéristique d'entrée, où
  • \(x_i ∈ X \)
  • \(y_i ∈ Y \)
  • \(|X| = l \)
  • \(|Y| = k \)
  • \(l >= k\)

Classificateurs

• Algorithme de classification
• Deux types de classificateurs:
  • Classificateurs binaires attribue un objet à l'une des deux classes
  • Classificateurs multiclasses attribue un objet à une ou plusieurs classes

Classification binaire

Linear Classificateurs

• Fonction linéaire attribuant un score à chaque catégorie possible en combinant le vecteur de caractéristiques d'une instance avec un vecteur de poids, en utilisant un produit de points.
• Formalisation :
  • Soit X être l'espace de saisie des caractéristiques et x_i ∈ X
  • Soit β_k un vecteur de poids pour la catégorie k
  • score(x_i, k) = x_i.β_k, score pour l'attribution de la catégorie k à l'instance x_i. La catégorie qui donne le score le plus élevé est attribuée à la catégorie de l'instance.

Évaluation

Dans le contexte de la classification en apprentissage machine, l'évaluation des performances d'un modèle implique la compréhension de différents types de prédictions qu'il peut faire par rapport à la réalité. Les vrais positifs (VP) et les vrais négatifs (VN) sont deux de ces éléments.

• Vrais Positifs (VP/TP) : Les vrais positifs représentent les cas où le modèle prédit correctement la classe positive. En d'autres termes, il a correctement identifié les exemples qui appartiennent réellement à la classe que le modèle essaie de prédire.
• Vrais Négatifs (VN/FN) : Les vrais négatifs représentent les cas où le modèle prédit correctement la classe négative. Cela signifie qu'il a correctement identifié les exemples qui n'appartiennent pas à la classe que le modèle essaie de prédire.

Évaluation

Évaluation

Soit

• tp: nombre de vrais postifs
• fp: nombre de faux positifs
• fn: nombre de faux négatifs

Évaluation

La précision mesure la proportion de prédictions positives faites par le modèle qui étaient effectivement correctes, tandis que le rappel mesure la proportion d'exemples positifs réels qui ont été correctement identifiés par le modèle. Alors

• Précision \[p = \frac{tp}{(tp + fp)}\]
• Rappel (Recall) \[r = \frac{tp}{(tp + fn)}\]

Évaluation

Le F1-score est la moyenne harmonique de la précision et du rappel. Il fournit une mesure globale de la performance d'un modèle de classification, tenant compte à la fois de la précision et du rappel. Il est particulièrement utile lorsque les classes sont déséquilibrées.

• F1-score \[f1 = 2 * \frac{(p * r)}{(p + r)}\]
• F1-score: meilleure valeur à 1 (précision et rappel parfaits) et pire à 0.

Le F1-score tient compte à la fois des erreurs de type I (faux positifs) et des erreurs de type II (faux négatifs), fournissant ainsi une mesure équilibrée de la performance du modèle.

Évaluation

• \(F_\beta\)-score utilise un facteur réel positif β, où β est choisi de telle sorte que le rappel est considéré comme β fois plus important que la précision, est :
• \(F_\beta\)-score \[F_\beta = (1 + \beta^2) \cdot \frac{\mathrm{p} \cdot \mathrm{r}}{(\beta^2 \cdot \mathrm{p}) + \mathrm{r}}\]
• Exemple: \(F_2\) score: Cette métrique est souvent utilisée dans des situations où le rappel est jugé plus critique que la précision, par exemple, dans des tâches où la détection des exemples positifs est particulièrement importante, même si cela entraîne un nombre plus élevé de faux positifs.

Le \(F_2\)-score est souvent utilisé dans des domaines où le rappel est considéré comme plus critique que la précision.

• Détection de Maladies : Dans le domaine médical, en particulier pour la détection de maladies graves, le F2-score peut être utilisé pour évaluer la performance des modèles. Il est crucial d'identifier correctement autant de cas positifs que possible, même si cela conduit à quelques faux positifs.
• Sécurité et Détection d'Intrusion : Lors de la détection d'intrusions dans les systèmes informatiques, il est souvent plus important de minimiser les faux négatifs (intrusions manquées) au profit de quelques faux positifs, d'où l'utilisation du F2-score.

• Recherche Biomédicale : Dans des domaines de recherche biomédicale où la découverte de certaines caractéristiques ou protéines spécifiques est critique, le F2-score peut être privilégié pour s'assurer que ces éléments sont correctement identifiés.
• Prévision de Catastrophes Naturelles : Lors de la prévision de catastrophes naturelles comme les tremblements de terre ou les tsunamis, il est essentiel de minimiser les faux négatifs pour garantir que le maximum d'avertissements est donné, même au prix de quelques alertes erronées.
• Recherche en Astronomie : Dans la recherche astronomique, la découverte de nouveaux objets célestes ou de phénomènes rares peut être cruciale. Le F2-score peut être utilisé pour évaluer les performances des algorithmes de détection.

Évaluation: matrice de confusion

La matrice de confusion est un outil essentiel dans l'évaluation des performances d'un système de classification. Elle fournit une vue détaillée des prédictions faites par le modèle par rapport aux classes réelles.

• Chaque ligne de la matrice représente les instances d'une classe prédite.
• Chaque colonne représente les instances d'une classe réelle.
• Toutes les prédictions correctes sont situées dans la diagonale du tableau.
• Les erreurs de prédiction sont représentées par des valeurs situées en dehors de la diagonale principale.

Évaluation: matrice de confusion

Évaluation: matrice de confusion

Classification binaire

Classification multiclasse

Classification multiclasse [Aly 2005]

• Transformation en classification binaire :
  • L'approche un contre le reste (Un contre tous) : Chaque classe est traitée comme une classe positive et toutes les autres comme une classe négative.
  • L'approche un-contre-un : Un classifieur binaire est construit pour chaque paire de classes.
• Extension de la classification binaire :
  • Réseaux de neurones : Adaptation des architectures pour prédire plusieurs classes simultanément.
  • k-voisins les plus proches : Extension de l'algorithme pour gérer plusieurs classes.
• Classification hiérarchique. : Organisation des classes dans une structure arborescente pour une classification plus fine et précise.

One-vs.-rest (One-vs.-all) strategy

One-vs.-rest (One-vs.-all) strategy

• Entraîner un seul classificateur par classe, avec les échantillons de cette classe comme échantillons positifs et tous les autres comme négatifs.
• Chaque classificateur produit un score de confiance réel pour sa décision

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

• Entrées :
  • \(L\), un apprenant (algorithme d'entraînement pour les classificateurs binaires)
  • échantillons \(X\)
  • étiquettes \(y\), où \(y_i ∈ \{1,..,K \} \) est l'étiquette de l'échantillon \(X_i\)
• Sortie :
  • une liste de classificateurs \(f_k\), où \(k ∈ \{1,..,K \} \)

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

Prendre des décisions signifie appliquer tous les classificateurs à un échantillon invisible x et prédire l'étiquette k pour laquelle le classificateur correspondant rapporte le score de confiance le plus élevé : \[\hat{y} = \underset{k \in \{1 \ldots K\}}{\arg\!\max}\; f_k(x)\]

One-vs.-one strategy

One-vs.-one strategy

2.2.2.1. Introduction

• Partitionnement de données est le processus de division d'un ensemble de données en différents sous-ensembles homogènes ou groupes.
• Objectif : Regrouper les données partageant des caractéristiques similaires dans chaque sous-ensemble.

Applications

• Analyse des réseaux sociaux : Identifier des communautés ou des groupes d'individus ayant des liens ou des intérêts similaires. Exemple : Regrouper des utilisateurs de réseaux sociaux en fonction de leurs interactions ou de leurs centres d'intérêt communs.
• Segmentation d'image : Diviser une image en régions homogènes selon des critères prédéfinis. Exemple : Identifier automatiquement les objets ou les régions d'intérêt dans une photographie.
• Systèmes de recommandation : Regrouper les utilisateurs ou les produits en fonction de leurs caractéristiques ou de leurs préférences. Exemple : Suggérer des produits ou des contenus similaires à des utilisateurs en se basant sur leurs historiques d'achats ou de navigation.

Définition formelle

• Soit \(X\) être l'espace de saisie des caractéristiques
• L'objectif du regroupement est de trouver \(k\) des sous-ensembles de \(X\), de façon à ce que

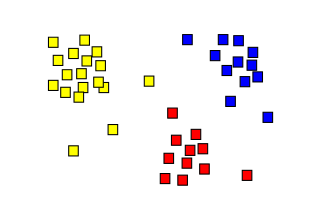
\[ C_1.. ∪ ..C_k ∪ C_{outliers} = X \] et

\[ C_i ∩ C_j = ϕ, i ≠ j; 1 <i,j <k \]

\(C_{outliers}\) peut consister en des cas extrêmes (anomalie de données)

Modèles de regroupement

• Modèles de centroïdes : Les groupes sont représentés par un seul vecteur moyen (centroïde). Exemple : K-Means, K-Médian.
• Modèles de connectivité : Les regroupements sont déterminés par la proximité de la connectivité entre les points. Exemple : Agglomératif Hiérarchique.
• Modèles de distribution : Les regroupements sont modélisés à l'aide de distributions statistiques. Exemple : Mélanges de Gaussiennes.
• Modèles de densité : Les regroupements sont définis par des régions denses connectées dans l'espace de données. Exemple : DBSCAN, OPTICS.

Modèles de regroupement

• Modèles de sous-espace : Identifient des regroupements dans des sous-espaces spécifiques des données. Exemple : CLIQUE, Subspace Clustering.
• Modèles de groupes : Organisent les données en groupes selon des critères spécifiques. Exemple : K-Modes pour les données catégoriques.
• Modèles graphiques : Utilisent des structures de graphes pour représenter les relations entre les données. Exemple : Algorithme de Marche Aléatoire pour la découverte de communautés.
• Modèles neuronaux : Utilisent des réseaux de neurones pour apprendre et découvrir des structures dans les données. Exemple : Autoencodeurs pour la réduction de dimensionnalité non linéaire.

Modèles de regroupement

Modèles de regroupement

2.2.3 Régression

• Processus visant à trouver une fonction mathématique qui modélise les relations entre les variables. L'objectif est d'estimer les relations et prédire les valeurs d'une variable en fonction d'autres variables.
• Fonction de modélisation : Trouver une fonction qui représente au mieux les données observées avec l'objectif de prédire ou estimer les valeurs d'une variable cible en fonction des variables explicatives.
• Analyse des relations : Examiner la relation entre une variable cible et une ou plusieurs variables explicatives. Méthodes : Identifier les tendances, les corrélations et les dépendances entre les variables.
• Attribution de valeurs : Assigner des valeurs réelles à chaque entrée pour modéliser les phénomènes du monde réel.

Applications

• Prévisions météorologiques : Prédire les conditions météorologiques futures en fonction des données historiques et des variables environnementales. Exemple : Estimation de la température, des précipitations et des vents pour les prochains jours.
• Prévisions de ventes : Estimer les ventes futures en fonction des tendances passées, des saisons et des stratégies marketing. Exemple : Prédiction des ventes de produits pour une période donnée.
• Apprentissage machine : Utiliser la régression comme composante d'algorithmes d'apprentissage machine pour la prédiction et la classification. Exemple : Modèles de régression linéaire dans les méthodes d'apprentissage supervisé.
• Finance : Évaluer les performances financières, prédire les prix des actions et des actifs, et estimer les risques. Exemple : Modèles de régression pour prédire les rendements financiers ou évaluer les risques de crédit.

Définition formelle

• La régression est représentée par une fonction qui associe un élément de données à une variable de prédiction.
• Elle peut être exprimée en termes de variables indépendantes \(X\), de variables dépendantes \(Y\) et de paramètres inconnus \(β\).
• Le modèle de régression vise à approximer la relation entre \(X\) et \(Y\) avec une fonction \(f(X, β)\), où \(β\) représente les paramètres du modèle.
• L'objectif est d'obtenir une approximation \(Y ≈ f(X, β)\) qui minimise l'écart entre les valeurs prédites et les valeurs observées.

Régression linéaire

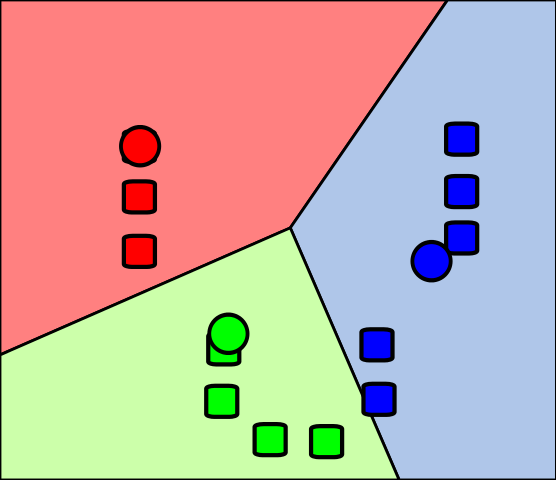
La régression linéaire est un modèle mathématique qui représente une relation linéaire entre une variable indépendante \(x_i\) et une variable dépendante \(y_i\). Le modèle a une forme d'une ligne droite (pour la régression linéaire simple) ou d'une parabole (pour la régression linéaire multiple).

• ligne droite: \(y_i = β_0 + β_1x_i + ε_i\) où \(β_0\) et \(β_1\) sont les coefficients de régression, \(x_i\) est la variable indépendante, et \(ε_i\) est l'erreur résiduelle.
• parabole: \(y_i = β_0 + β_1x_i + β_2x_i^2 +ε_i\) où \(β_0\), \(β_1\), et \(β_2\) sont les coefficients de régression pour chaque terme, \(x_i\) est la variable indépendante, et \(ε_i\) est l'erreur résiduelle.

Régression linéaire

Ligne droite: \(y_i = β_0 + β_1x_i + ε_i\) où \(β_0\) et \(β_1\) sont les coefficients de régression, \(x_i\) est la variable indépendante, et \(ε_i\) est l'erreur résiduelle.

Pour minimiser l'erreur :

• Calcul des prédictions : \( ŷ_i = β_0 + β_{1}x_i \)
• Calcul des résidus: \(e_i = ŷ_i - y_i\)
• Calcul de la somme des carrés des résidus (SSE) pour évaluer l'ajustement du modèle., \(SSE = Σ e_i\), where \(1 < i < n\)

L'objectif est de minimiser SSE pour obtenir la meilleure approximation de la relation linéaire entre les variables.

Processus consistant à attribuer une classe ou une étiquette à chaque élément d'une séquence de valeurs ou de tokens. Exemple : Reconnaissance d'entités nommées (NER) avec spaCy, où des entités comme les noms de personnes, les lieux, ou les organisations sont identifiées et étiquetées dans un texte.

spaCy: Reconnaissance d'entités nommées

Reconnaissance d'entités nommées (spaCy)

Applications

• Etiquetage de la partie du discours : Assigner des étiquettes grammaticales à chaque mot d'une phrase pour analyser sa structure syntaxique.
• Traduction linguistique : Identifier et étiqueter les mots ou phrases dans une langue source avant leur traduction dans une langue cible.
• Analyse vidéo : Marquer et catégoriser les actions ou objets identifiés dans une séquence vidéo.
• Reconnaissance de l'écriture manuscrite : Attribuer des étiquettes à chaque caractère ou symbole écrit à la main pour la reconnaissance de texte.
• Extraction d'informations : Identifier et étiqueter des éléments d'intérêt dans un document ou un ensemble de données pour extraire des informations pertinentes.

Définition formelle

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• Soit \(〈x_1,...,x_T〉\) une séquence de longueur \(T\).
• L'objectif de l'étiquetage des séquences est de générer une séquence correspondante
  • \(〈y_1,...,y_T〉\) des étiquettes
  • \(x_i ∈ X\)
  • \(y_j ∈ Y\)

Association Rules

Les règles d'association, également connues sous le nom de "Association Rules", sont un ensemble de techniques d'analyse de données visant à découvrir les relations et les associations entre les variables dans un ensemble de données. Cette méthode recherche des corrélations et des co-occurrences entre les éléments, permettant ainsi de dégager des motifs ou des modèles significatifs.

Un exemple courant d'application des règles d'association est l'analyse de paniers d'achats dans le domaine du commerce de détail, où ces règles sont utilisées pour identifier des schémas d'achat, tels que les combinaisons de produits souvent achetés ensemble.

Association Rules

Prenons un exemple concret avec un tableau de données représentant les transactions d'une épicerie :

Association Rules

Dans ce tableau, chaque colonne représente un produit et chaque ligne représente une transaction. Un "1" indique que le produit a été acheté lors de cette transaction, tandis qu'un "0" indique que le produit n'a pas été acheté.

Applications

• Exploitation de l'utilisation du web : Utilisées pour analyser les comportements des utilisateurs en ligne, personnaliser les recommandations de produits et cibler les publicités.
• Détection d'intrusion : Utilisées en sécurité informatique pour repérer les comportements malveillants et détecter les tentatives d'intrusion.
• Analyse d'affinité : Utilisées dans le marketing pour identifier les relations entre les produits souvent achetés ensemble, permettant ainsi de recommander des produits complémentaires et de créer des offres groupées attractives.

Définition formelle

• Soit \(I\) un ensemble de \(n\) attributs binaires appelés items
• Soit \(T\) un ensemble de \(m\) transactions appelé base de données
• Soit \(I\) = \(\{(i_1,...,i_n)\}\) et \(T\) = \({(t_1,...,t_m)}\)
• L'objectif de l'apprentissage des règles d'association est de trouver
  • \(X ⇒ Y\), where \(X ⇒ Y ⊆ I\)
  • \(X\) est l'antécédent
  • \(Y\) est la conséquence

Une règle d'association \(X ⇒ Y\) est valide si le support et la confiance de la règle dépassent les seuils spécifiés. Cela signifie que \(X\) et \(Y\) apparaissent fréquemment ensemble dans les transactions, et que lorsque \(X\) est présent, \(Y\) est également souvent présent.

Support

Le support d'un ensemble d'articles dans le contexte des règles d'association est défini comme la fréquence à laquelle cet ensemble d'articles apparaît dans la base de données. En d'autres termes, c'est le nombre de transactions dans lesquelles cet ensemble d'articles est présent, divisé par le nombre total de transactions dans la base de données. Le support mesure donc la popularité ou la prévalence d'un ensemble d'articles. Il est utilisé pour évaluer à quel point une association entre deux ensembles d'articles est forte. Une valeur élevée de support indique que l'association est fréquente dans la base de données, ce qui la rend potentiellement plus significative.

\[supp(X) = \frac{|t ∈T; X ⊆ t|}{ |T|}\]

Confidence

La confidence dans le contexte des règles d'association représente la fréquence à laquelle la règle a été trouvée vraie dans la base de données. Plus précisément, elle mesure la probabilité conditionnelle que la conséquence Y se produise dans une transaction, étant donné que l'antécédent X est également présent dans cette transaction.

La confidence d'une règle est calculée en divisant le nombre de transactions dans lesquelles à la fois X et Y sont présents par le nombre de transactions dans lesquelles X est présent. Ainsi, une confidence élevée indique que la conséquence Y est souvent vraie lorsque l'antécédent X est présent, ce qui renforce la fiabilité de la règle d'association.

\[conf(X ⇒ Y) = \frac{supp(X ∪ Y)}{supp(X)}\]

En utilisant les règles d'association, nous pouvons extraire des relations significatives entre les produits. Par exemple, en appliquant un support minimum de 40% et un seuil de confiance de 60%, nous pouvons identifier les règles d'association suivantes :

1. {Pain, Lait} \( ⇒\) {Œufs} (Support : 40%, Confiance : 100%)
2. {Lait} \( ⇒\) {Œufs} (Support : 60%, Confiance : 75%)
3. {Œufs} \( ⇒\) {Lait} (Support : 60%, Confiance : 75%)

Cela signifie que dans 40% des transactions, les clients ont acheté du pain et du lait ensemble, et dans 100% de ces transactions, ils ont également acheté des œufs. De même, dans 60% des transactions, les clients ont acheté du lait, et dans 75% de ces transactions, ils ont également acheté des œufs.

Lift

Le lift dans le contexte des règles d'association est le rapport entre le "support" observé de la règle et celui attendu si les ensembles d'items X et Y étaient indépendants.Formellement, le lift est calculé en divisant le support de la règle par le produit des supports individuels de X et Y. En d'autres termes, c'est la mesure de combien plus fréquemment la règle est observée que ce à quoi on s'attendrait si les événements X et Y étaient indépendants.

Un lift supérieur à 1 indique que la règle a une association positive entre X et Y (c'est-à-dire que les items X et Y apparaissent ensemble plus fréquemment que prévu au hasard), tandis qu'un lift inférieur à 1 indique une association négative ou non significative. Un lift de 1 indique une indépendance entre les items X et Y.

• \[lift(X ⇒ Y) = \frac{supp(X ∪ Y)}{(supp(X) ⨉ supp(Y))}\]

La détection d'anomalies, également connue sous le nom de détection des valeurs aberrantes, implique l'identification de données inhabituelles ou divergentes dans un ensemble de données. Voici quelques approches courantes pour détecter les anomalies :

• Détection supervisé : le modèle est entraîné sur un ensemble de données étiqueté avec des exemples d'anomalies et de données normales. Le modèle est ensuite utilisé pour prédire si de nouvelles données sont anormales ou normales en fonction de ces étiquettes.
• Détection non-supervisé : Contrairement à la détection supervisée, cette approche n'utilise pas d'étiquettes dans l'ensemble de données d'entraînement. Au lieu de cela, elle identifie les anomalies en examinant les caractéristiques statistiques des données et en recherchant des points de données qui diffèrent significativement du reste de l'ensemble de données.
• Détection semi-supervisé : Cette approche combine des éléments des deux méthodes précédentes. Elle utilise à la fois des données étiquetées et non étiquetées pour entraîner le modèle. Cela peut être utile lorsque seules quelques anomalies sont disponibles pour l'entraînement, mais que l'ensemble de données est principalement non étiqueté.

Applications

• Détection d'intrusion : Identifier les activités malveillantes ou non autorisées dans les réseaux informatiques pour protéger les systèmes contre les cyberattaques.
• Détection de fraude : Repérer les transactions financières suspectes ou les activités frauduleuses dans les transactions en ligne, les cartes de crédit, ou les assurances.
• System health monitoring : Surveiller en continu la santé des systèmes informatiques, des machines industrielles ou des équipements médicaux pour détecter les pannes ou les défaillances potentielles.
• Détection d'événements dans les réseaux de capteurs : Identifier les événements inhabituels ou les comportements anormaux dans les réseaux de capteurs environnementaux, tels que la surveillance de la qualité de l'air ou la détection des intrusions dans les systèmes de sécurité.
• Détection d'abus dans un système d'information : Identifier les utilisateurs ou les activités qui abusent ou enfreignent les politiques de sécurité dans les systèmes d'information, les applications en ligne ou les plateformes de réseaux sociaux.

Caractéristiques

Des sursauts inattendus : Les anomalies peuvent se manifester sous forme de sursauts ou de pointes inattendues dans les données. Par exemple, une augmentation soudaine du trafic sur un site Web peut indiquer une attaque de déni de service (DDoS) dans le cas de la surveillance du trafic réseau, ou une augmentation anormale des transactions financières peut signaler une fraude.

Les caractéristiques des données varient selon le domaine d'application et les types spécifiques d'anomalies recherchées. Identifiez les schémas inhabituels ou les comportements aberrants dans les données peut aider à détecter les anomalies et à prendre des mesures appropriées pour les gérer.

Formalisation

• Soit \(Y\) un ensemble de mesures. Cela représente les données ou les variables observées qui sont surveillées pour détecter les anomalies.
• Soit \(P_Y(y)\) un modèle statistique pour la distribution des \(Y\) dans des conditions "normales". Les données normales sont généralement modélisées par une distribution statistique telle que la distribution normale (gaussienne). Ce modèle est utilisé pour estimer la probabilité que les données observées soient normales.
• Soit \(T\) un seuil défini par l'utilisateur. C'est une valeur seuil fixée par l'utilisateur qui détermine à partir de quelle probabilité une mesure est considérée comme anormale. Les mesures dont la probabilité estimée est inférieure à ce seuil sont considérées comme des anomalies.
• Une mesure \(x\) est une valeur isolée si \(P_Y(x) < T\). Cette condition spécifie que si la probabilité d'une mesure est inférieure au seuil défini, cette mesure est considérée comme isolée ou anormale par rapport aux autres observations.

• Synthèse courte d'un ensemble de données : Elle consiste à résumer de manière concise les principales caractéristiques et tendances des données. Cela peut inclure des statistiques descriptives telles que la moyenne, la médiane, l'écart-type, ainsi que des visualisations récapitulatives comme des histogrammes, des graphiques linéaires ou des diagrammes à barres. L'objectif est de fournir une vue d'ensemble rapide et informative des données.
• Génération de rapports : la génération de rapports peut être utilisée pour communiquer efficacement les informations clés aux parties prenantes. Ces rapports peuvent prendre différentes formes, telles que des documents écrits, des présentations visuelles ou des tableaux de bord interactifs. L'accent est mis sur la clarté, la concision et la pertinence des informations présentées pour aider les décideurs à prendre des décisions éclairées.

Applications

• Extraction des mots-clès : Identifier les mots ou expressions clés dans un texte ou un ensemble de documents pour résumer leur contenu de manière succincte.
• Récapitulation de documents : Résumer le contenu et les principales idées d'un document ou d'un ensemble de documents pour en faciliter la compréhension et l'assimilation.
• Moteurs de recherche : Fournir des résumés pertinents des pages Web ou des résultats de recherche afin d'aider les utilisateurs à trouver rapidement les informations qu'ils recherchent.
• Récapitulation d'images : Extraire les caractéristiques importantes d'une image pour résumer son contenu ou en faciliter la recherche et la classification.
• Récapitulation de vidéos : Identifier et résumer les événements principaux ou les moments saillants dans une vidéo pour permettre aux utilisateurs de naviguer rapidement dans le contenu et de trouver des informations spécifiques.

Formalisation: Synthèse multi-documents

• Soit \(\{D = D_1, ..., D_k\}\) une collection de \(k\) documents
• Un document \(\{D = t_1, ..., t_m\}\) se compose de m unités textuelles (mots, phrases, paragraphes, etc.)
• Soit \(\{D = t_1, ..., t_n\}\) être l'ensemble complet de toutes les unités textuelles de tous les documents, où
  • \(t_i ∈ D\), si et seulement si \(∃ D_j\) de sorte que \(t_i ∈ D_j\)
• \(S ⊆ D\) constitue une synthèse
• Deux fonctions de scoring
  • \(Rel(i)\): pertinence de l'unité textuelle \(i\) dans le résumé
  • \(Red(i,j)\): Redondance entre deux unités textuelles \(t_i, t_j\)

Formalisation: Multidocument summarization

• La note pour un résumé \(S\)
  • \(s(S)\) note pour un résumé S
  • \(l(i)\) est la longueur de l'unité textuelle \(i\)
  • \(K\) est la longueur maximale fixée du résumé

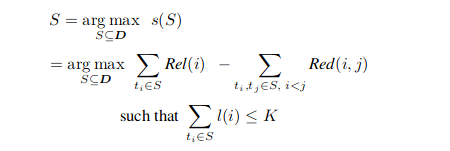
Trouver un sous-ensemble à partir de l'ensemble du sous-ensemble.

1. Extraction: Cette approche implique la sélection d'un sous-ensemble de mots, de phrases ou d'expressions existants dans le texte original sans aucune modification. L'objectif est de repérer les parties les plus importantes du texte et de les présenter de manière concise dans le résumé. Les techniques utilisées dans cette approche incluent l'identification de phrases clés, la classification des phrases par importance, et l'extraction de phrases représentatives.
2. Abstraction: Contrairement à l'extraction, l'approche d'abstraction implique la construction d'une représentation sémantique interne du texte, suivie de l'utilisation de techniques de génération du langage naturel pour produire un résumé. Cela nécessite une compréhension plus profonde du contenu du texte et la capacité de reformuler les idées de manière concise tout en préservant leur signification. Les techniques d'abstraction peuvent inclure la réécriture de phrases, la fusion d'informations similaires et la génération de paraphrases.

Résumé extractif

1. Résumé générique: Cette approche vise à obtenir un résumé général et représentatif du contenu original en extrayant les informations les plus importantes et les plus pertinentes. Elle cherche à capturer l'essence du texte original en identifiant les phrases ou les sections clés qui révèlent les principaux points et concepts abordés. Ce type de résumé est souvent utilisé dans des contextes où une vue d'ensemble est nécessaire sans se concentrer sur des aspects spécifiques ou des détails.
2. Résumé pertinent pour la recherche : Cette approche vise à produire un résumé qui répond spécifiquement aux besoins ou aux intérêts d'un utilisateur ou d'une tâche de recherche particulière. Elle utilise des techniques de sélection de phrases basées sur la pertinence pour extraire les parties du texte qui correspondent aux critères de recherche spécifiques de l'utilisateur. Cela permet de fournir des résumés plus ciblés et adaptés aux besoins individuels, ce qui peut être particulièrement utile dans les domaines où la précision et la pertinence sont essentielles, comme la recherche d'informations spécialisées ou la prise de décision.

1. Support Vector Machines (SVM)
2. Descente du gradient stochastique
3. Voisins proches
4. Bayes naïfs
5. Arbres de décision
6. Ensemble Methods (Forêt d'arbres décisionnels)

Introduction

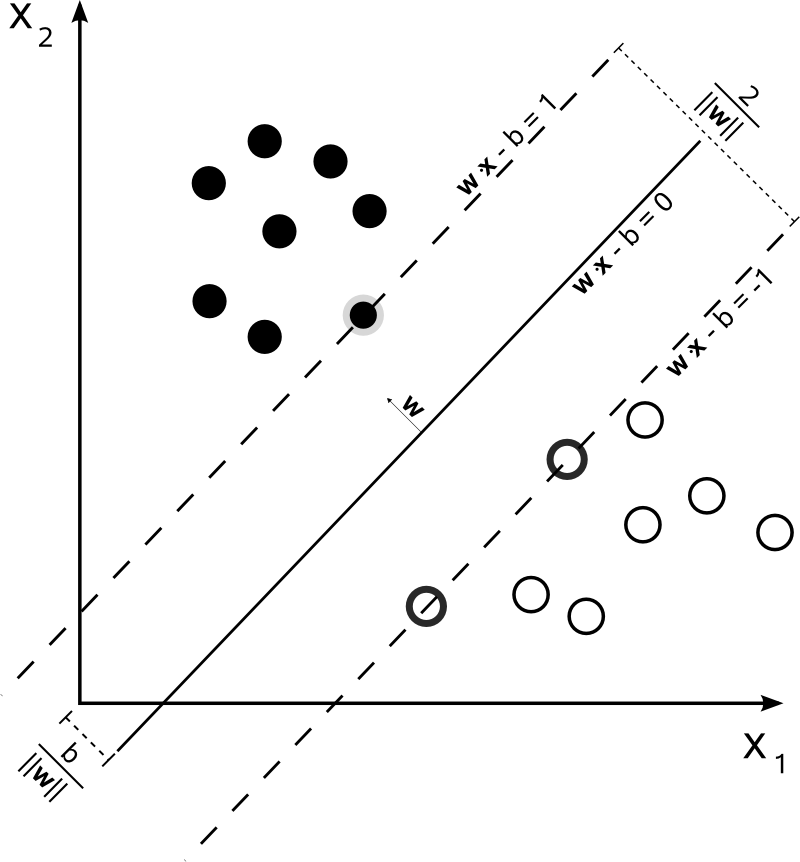
La machine à vecteurs de support (SVM) est une méthode d'apprentissage supervisé. SVM cherche à trouver la meilleure frontière de décision qui optimise la séparation des classes, ce qui permet une classification précise même dans des espaces de données complexes.

• Elle est principalement utilisée pour la classification binaire, bien qu'elle puisse être étendue à des problèmes de classification multiclasse.
• L'objectif principal de SVM est de construire un hyperplan qui maximise la marge de séparation entre les deux classes. L'hyperplan est la frontière de décision qui sépare les données en deux classes distinctes.

Hyperplane

L'hyperplan dans l'espace n-dimensionnel est un sous-espace de dimension n-1 qui permet de séparer les données en deux classes.

• Dans un espace à deux dimensions, l'hyperplan est une ligne à une dimension qui sépare les données en deux régions.
• Dans un espace tridimensionnel, l'hyperplan est un plan bidimensionnel qui divise l'espace en deux parties distinctes.
• L'hyperplan d'un espace tridimensionnel est un plan bidimensionnel

Définition formelle

• Le but d'un SVM est d'estimer une fonction \(f: R^N ⨉ {+1,-1}\), c'est à dire,
  • Si \(x_1,...,x_l\) ∈ \(R^N\) sont les \(N\) points de données d'entrée,
  • L'objectif est de trouver \((x_1,y_1),...,(x_l,y_l)\) ∈ \(R^N ⨉ {+1,-1}\)
• Tout hyperplan peut être écrit par l'équation en utilisant un ensemble de points d'entrée \(x\)
  • \(w.x - b = 0\), où
  • \(w ∈ R^N\), un vecteur normal à la plane
  • \(b ∈ R\)
• Une fonction de décision est donnée par \(f(x) = sign(w.x - b )\)

Définition formelle

• Si les données de formation sont séparables linéairement, deux hyperplans peuvent être sélectionnés
• Ils séparent les deux classes de données,
  afin que la distance entre elles soit la plus grande possible.
• Les hyperplans peuvent être donnés par les équations
  • \(w.x - b = 1\)
  • \(w.x - b = -1\)

Définition formelle

• La distance entre les deux hyperplans peut être donnée par \( \frac{2}{||w||} \)
• La région située entre ces deux hyperplans est appelée marge.
• L'hyperplan à marge maximale est l'hyperplan
  qui se trouve à mi-chemin entre eux.

Définition formelle

• Afin d'éviter que les points de données ne tombent dans la marge, les contraintes suivantes sont ajoutées
  • \(w.x_i - b >= 1\), si \(y_i = 1\)
  • \(w.x_i - b <= -1\), si \(y_i = -1\)
• \(y_i(w.x_i - b) >= 1\), \(1<= i <= n\)
• L'objectif est de minimiser ||w|| sous réserve de \(y_i(w.x_i - b) >= 1\), \(1<= i <= n\)
• Une solution pour les deux \(w\) et \(b\) donne le classificateur \(f(x) = sign(w.x - b)\)
• L'hyperplan à marge maximale est entièrement déterminé par les points qui en sont les plus proches, appelés vecteurs de soutien

Data mining

• Classification : SVM peut être utilisée pour la classification binaire ainsi que pour la classification multi-classes, où elle cherche à séparer les données en plusieurs catégories distinctes en construisant des hyperplans dans un espace multidimensionnel.
• Régression : SVM peut également être appliquée à des problèmes de régression, où elle cherche à prédire une valeur continue plutôt que de classer des données en catégories discrètes.
• Détection des anomalies : SVM peut être utilisée pour détecter les anomalies dans les données en identifiant les points de données qui sont significativement différents du reste de l'ensemble de données, ce qui en fait un outil précieux pour la détection des fraudes ou des erreurs dans les données.

Applications

• Catégorisation des textes et des hypertextes : Les SVM sont largement utilisées pour classer automatiquement les documents texte dans différentes catégories, comme la classification des courriels en spam ou en non-spam, la catégorisation des articles de presse, etc.
• Classification des images : SVM est efficace pour classer des images dans des catégories prédéfinies, comme la classification des images médicales en différentes maladies, la reconnaissance des visages, la détection d'objets dans des images, etc.
• Reconnaissance de l'écriture manuscrite : SVM est également utilisée dans les systèmes de reconnaissance de l'écriture manuscrite pour identifier les caractères ou les mots écrits à la main et les transcrire en texte numérique.

Le gradient stochastique de descente est une technique d'optimisation utilisée pour minimiser une fonction objective qui peut être exprimée comme une somme de fonctions différenciables.

• Il s'agit d'une approximation stochastique de l'optimisation de la descente du gradient, où le calcul du gradient est effectué de manière aléatoire sur un sous-ensemble des données à chaque itération.
• Cette méthode est itérative, ce qui signifie qu'elle effectue des mises à jour progressives des paramètres du modèle pour se rapprocher du minimum ou du maximum de la fonction objectif.
• Le gradient stochastique de descente est particulièrement efficace pour traiter de grands ensembles de données, car il permet de calculer les mises à jour des paramètres de manière incrémentielle, ce qui réduit la charge de calcul par rapport à l'optimisation classique du gradient.

Gradient

Le gradient est une généralisation multi-variable de la notion de dérivée.

• Le gradient donne la pente de la tangente du graphe d'une fonction à un point donné dans l'espace multi-dimensionnel. Il indique dans quelle direction et dans quelle mesure la fonction augmente ou diminue le plus rapidement à partir de ce point.

Gradient

• Dans le cas des fonctions à plusieurs variables, le gradient est un vecteur qui contient les dérivées partielles de la fonction par rapport à chacune de ses variables. Chaque composante du gradient correspond à la pente de la fonction dans la direction respective de la variable correspondante.

Gradient

• Géométriquement, le gradient pointe dans la direction du plus grand taux d'augmentation de la fonction. En d'autres termes, il indique la direction dans laquelle la fonction croît le plus rapidement à partir du point considéré.
• L'amplitude du gradient représente la pente du graphique de la fonction dans la direction indiquée par le gradient. Plus cette amplitude est grande, plus la fonction augmente rapidement dans cette direction.

Gradient ou dérivé

Algorithme du gradient

L'algorithme du gradient stochastique de descente est un algorithme d'optimisation itératif largement utilisé pour trouver le minimum d'une fonction.

1. Initialisation : Choisissez un point de départ aléatoire ou prédéfini dans l'espace des paramètres.
2. Calcul du gradient : Calculez le gradient de la fonction objective par rapport aux paramètres au point courant.

Algorithme du gradient

3. Mise à jour des paramètres : Mettez à jour les paramètres dans la direction opposée au gradient. Cela implique de soustraire une fraction du gradient de chaque paramètre.
4. Répétition : Répétez les étapes 2 et 3 jusqu'à ce qu'un critère d'arrêt soit satisfait, par exemple, un nombre fixe d'itérations, une petite variation de la fonction objective ou une tolérance pour le gradient.

Algorithme du gradient

L'algorithme stochastique du gradient de descente est une variante où le gradient est calculé de manière stochastique, c'est-à-dire qu'au lieu d'utiliser l'ensemble complet des données pour calculer le gradient à chaque itération, un sous-ensemble aléatoire ou une seule observation est utilisé. Cela permet de gagner en efficacité, en particulier pour les grands ensembles de données.

L'objectif principal de cet algorithme est de minimiser une fonction objective, souvent une fonction de perte dans le cadre de l'apprentissage automatique, et il est largement utilisé dans des domaines tels que l'optimisation convexe, l'apprentissage automatique et le traitement du signal.

Méthode standard de descente de gradient

• Prenons le problème de la minimisation d'une fonction objective
  • \(Q(w) = \frac{1}{n} (ΣQ_i(w)), 1<=i<n\)
  • \(Q_i(w)\) est la valeur de la fonction objectif pour le \(i\)-ème exemple.
  • \(Q(w)\) est le risque empirique.
• \(w = w - η.∇ Q(w)\)
• \(w = w - \frac{\eta}{n} \sum_{i=1}^n \nabla Q_i(w)\), \(\eta\) est le pas de l'itération

Méthode itérative

• Choisissez un vecteur initial de paramètres \(w\) et le taux d'apprentissage η.
• Répétez l'opération jusqu'à l'obtention d'un minimum approximatif :
  • Mélangez aléatoirement les exemples dans le jeu de formation.
  • \(w = w - η.∇ Q_i(w)\), \(i=1...n\)

Applications

• Classification : le SGD est souvent utilisé pour entraîner des modèles de classification tels que les machines à vecteurs de support (SVM), les réseaux de neurones et les modèles de régression logistique. Il permet de trouver les paramètres optimaux du modèle en minimisant une fonction de perte, ce qui conduit à une meilleure capacité de classification.
• Régression : Le SGD est également utilisé pour l'entraînement de modèles de régression, où l'objectif est de prédire une valeur continue en fonction d'un ensemble de variables explicatives. Il est couramment utilisé dans des domaines tels que l'analyse financière, la prédiction des prix et la modélisation des séries chronologiques.

La méthode des k plus proches voisins (kNN) et le partitionnement en k-moyennes (k-means clustering) sont deux techniques importantes en apprentissage automatique et en exploration de données :

1. Méthode des k plus proches voisins (kNN) : C'est un algorithme d'apprentissage supervisé utilisé pour la classification et la régression. L'idée principale derrière kNN est de trouver les k échantillons d'entraînement les plus proches du point de données de test et de prédire l'étiquette de classe en fonction de la classe majoritaire parmi ces voisins. Pour la régression, la prédiction est la moyenne des valeurs cibles des k voisins les plus proches.
2. Partitionnement en k-moyennes (k-means clustering) : C'est une méthode non supervisée de partitionnement de données en k groupes distincts. L'algorithme fonctionne en répétant deux étapes : d'abord, il attribue chaque point de données au groupe dont le centroïde est le plus proche, puis il met à jour les centroïdes en calculant la moyenne de tous les points attribués à chaque groupe. Ces étapes sont répétées jusqu'à ce qu'une convergence soit atteinte et que les centroïdes ne changent plus de manière significative.

Partitionnement en k-moyennes

• Méthode de partitionnement de données : Le partitionnement en k-moyennes vise à diviser un ensemble de données en k groupes (clusters) distincts. Chaque cluster est représenté par son centroïde, qui est la moyenne de tous les points appartenant à ce cluster.
• Entrée : L'entrée de l'algorithme est un ensemble de points de données ainsi que le nombre k de clusters souhaité. Ces points de données peuvent avoir plusieurs dimensions.
• Objectif : L'objectif principal du k-means clustering est de minimiser la variance intra-cluster, c'est-à-dire de minimiser la somme des distances au carré de chaque point par rapport à son centroïde assigné.

Partitionnement en k-moyennes

• Fonctionnement : L'algorithme k-means fonctionne en itérant entre deux étapes principales :
  • Attribution des points aux clusters : Chaque point de données est assigné au cluster dont le centroïde est le plus proche en termes de distance euclidienne.
  • Mise à jour des centroïdes : Une fois que tous les points ont été attribués à des clusters, les centroïdes de chaque cluster sont mis à jour en calculant la moyenne des points appartenant à ce cluster.
• Convergence : Les deux étapes ci-dessus sont répétées de manière itérative jusqu'à ce qu'une convergence soit atteinte, c'est-à-dire que les centroïdes ne changent plus significativement entre deux itérations successives.

Partitionnement en k-moyennes

Étape 1 (Initialisation)

Les "moyens", également appelés centroïdes, sont les points initiaux autour desquels les clusters seront formés. Dans cette étape, k points sont sélectionnés de manière aléatoire à partir de l'ensemble de données pour servir de moyens initiaux.

Partitionnement en k-moyennes

Étape 2 (Étape d'affectation)

Dans la deuxième étape de l'algorithme de partitionnement en k-moyennes (k-means clustering), également connue sous le nom d'étape d'affectation, les k clusters sont créés en associant chaque observation à la moyenne la plus proche.Les partitions représentent ici le diagramme de Voronoï généré par les moyennes.

Partitionnement en k-moyennes

Étape 2 (Étape d'affectation)

Partitionnement en k-moyennes

Étape 3 (Étape de mise à jour et calcul du centroïde)

Les centroids de chacun des k agrégats sont recalculés pour devenir les nouvelles moyennes.

Partitionnement en k-moyennes

Étape 3 (Étape de mise à jour et calcul du centroïde)

• Calcul du centroïde : Pour chaque cluster formé à l'étape précédente, le centroïde est calculé. Le centroïde est simplement la moyenne de toutes les observations qui appartiennent à ce cluster. Il est calculé en prenant la moyenne des coordonnées de toutes les observations dans le cluster, ce qui donne une position centrale représentative.
• Mise à jour des moyennes : Une fois que les centroïdes de tous les clusters ont été calculés, ils deviennent les nouvelles moyennes pour la prochaine itération de l'algorithme. Les anciennes moyennes sont alors remplacées par les nouveaux centroïdes.

Partitionnement en k-moyennes

Étape 4 (Répéter jusqu'à la convergence)

La quatrième étape de l'algorithme de partitionnement en k-moyennes (k-means clustering) consiste à répéter les étapes 2 et 3 jusqu'à ce que la convergence soit atteinte.

Partitionnement en k-moyennes

Étape 4 (Répéter jusqu'à la convergence)

• Répétition des étapes précédentes : Les étapes d'affectation (étape 2) et de mise à jour des moyennes (étape 3) sont répétées itérativement jusqu'à ce que la convergence soit atteinte. Cela signifie que les observations sont successivement associées aux clusters en fonction de leur proximité aux moyennes actuelles, puis les moyennes sont mises à jour en fonction des observations assignées à chaque cluster.
• Critère de convergence : L'algorithme a convergé lorsque les affectations ne changent plus entre les itérations successives. Cela signifie que les clusters ne subissent plus de changements significatifs et que les moyennes ne se déplacent plus de manière significative entre les itérations.
• Arrêt de l'algorithme : Une fois que la convergence est atteinte, l'algorithme s'arrête et les clusters finaux ainsi que leurs centroïdes associés sont considérés comme la solution de l'algorithme.

Méthode des k plus proches voisins

La méthode des k plus proches voisins (k-NN) est un algorithme d'apprentissage supervisé utilisé à la fois pour la classification et la régression.

• Classification k-NN : Dans ce cas, la sortie est une appartenance à une classe. Pour classer un nouvel objet, l'algorithme k-NN examine les k exemples les plus proches dans l'ensemble d'apprentissage et détermine la classe majoritaire parmi ces voisins. Plus précisément, chaque voisin contribue à un vote, et la classe la plus fréquente parmi les k voisins est attribuée à l'objet à classer. C'est un exemple de vote majoritaire parmi les voisins les plus proches.
• Régression k-NN : À la différence de la classification, dans la régression k-NN, la sortie est une valeur de propriété de l'objet. Pour prédire la valeur d'une nouvelle observation, l'algorithme k-NN calcule la valeur moyenne (ou médiane) des valeurs cibles des k plus proches voisins. Par conséquent, au lieu de voter pour une classe majoritaire, les valeurs cibles des k voisins sont utilisées pour prédire la valeur cible de l'objet à estimer.

Méthode des k plus proches voisins

Supposons que nous ayons un ensemble de données d'apprentissage composé de points dans un espace bidimensionnel, où chaque point est associé à une classe. Supposons que nous voulions classer un nouveau point avec des coordonnées (x = 4, y = 3).

Méthode des k plus proches voisins

1. Choix de k : Disons que nous choisissons k = 3.
2. Calcul de la distance : Nous calculons la distance euclidienne entre le nouveau point et chaque point de notre ensemble d'apprentissage.
   • - Pour le point A : Distance = sqrt((4 - 2)^2 + (3 - 3)^2) = sqrt(4) = 2
   • - Pour le point B : Distance = sqrt((4 - 4)^2 + (3 - 4)^2) = sqrt(1) = 1
   • - Pour le point C : Distance = sqrt((4 - 3)^2 + (3 - 2)^2) = sqrt(2) ≈ 1.41
   • - Pour le point D : Distance = sqrt((4 - 6)^2 + (3 - 5)^2) = sqrt(8) ≈ 2.83
   • - Pour le point E : Distance = sqrt((4 - 5)^2 + (3 - 3)^2) = sqrt(1) = 1

Méthode des k plus proches voisins

3. Sélection des k plus proches voisins : Nous identifions les k points les plus proches du nouveau point en termes de distance.
   • - Pour k = 3, les trois plus proches voisins sont B, C et E.
4. Vote majoritaire : Enfin, nous attribuons la classe majoritaire parmi les k voisins les plus proches au nouveau point. Dans ce cas, deux des voisins les plus proches (C et E) sont de la classe "Bleu" et un (B) est de la classe "Rouge". Par conséquent, le nouveau point est classé comme "Bleu".

Applications

• Régression : En utilisant la méthode des plus proches voisins pour la régression, on peut estimer la valeur d'une variable cible pour une nouvelle observation en prenant la moyenne des valeurs de la variable cible des k voisins les plus proches. Par exemple, dans la régression k-NN, on peut prédire le prix d'une maison en prenant la moyenne des prix des k maisons les plus proches en termes de caractéristiques similaires (surface, nombre de chambres, etc.).
• Détection des anomalies : La méthode des plus proches voisins peut également être utilisée pour détecter les anomalies dans les données. Les observations qui sont très différentes de leurs voisins les plus proches peuvent être considérées comme des anomalies. Par exemple, dans la surveillance de la santé, des valeurs de signes vitaux inhabituelles par rapport aux voisins les plus proches peuvent indiquer un problème de santé potentiel et donc être considérées comme des anomalies.

La classification naïve bayésienne est une méthode de classification probabiliste simple basée sur l'application du théorème de Bayes avec une forte hypothèse d'indépendance entre les caractéristiques.

• Théorème de Bayes : La classification naïve bayésienne repose sur le théorème de Bayes, qui est une formule pour calculer les probabilités conditionnelles. Il permet de calculer la probabilité qu'une observation appartienne à une classe donnée en utilisant les probabilités des caractéristiques étant donné chaque classe.

• Hypothèse d'indépendance naïve : La caractéristique principale de la classification naïve bayésienne est l'hypothèse d'indépendance naïve, qui suppose que les caractéristiques sont indépendantes les unes des autres conditionnellement à la classe. Cela signifie que la présence d'une caractéristique particulière dans une classe ne dépend pas de la présence d'autres caractéristiques.
• Modélisation des probabilités : Pour chaque classe, la classification naïve bayésienne modélise les distributions de probabilité des caractéristiques. Ensuite, lorsqu'une nouvelle observation est introduite, elle utilise le théorème de Bayes pour calculer la probabilité qu'elle appartienne à chaque classe et choisit la classe avec la probabilité la plus élevée.

Applications

• Classification des documents : Elle est largement utilisée pour la classification des documents, tels que la détection de spam (classification des e-mails en spam ou non-spam) et la catégorisation de documents dans différentes catégories.
• Analyse de sentiments : Dans le domaine du traitement du langage naturel, la classification naïve bayésienne est utilisée pour l'analyse des sentiments, où elle peut être utilisée pour classifier les textes en fonction de leur tonalité émotionnelle, comme positif, négatif ou neutre.
• Catégorisation de documents : Elle est également utilisée pour la catégorisation automatique de documents, où elle peut être utilisée pour classifier les documents dans des catégories spécifiques en fonction de leur contenu ou de leur sujet.
• Reconnaissance de caractères : Dans le domaine de la vision par ordinateur, la classification naïve bayésienne est utilisée pour la reconnaissance de caractères, où elle peut être utilisée pour classifier les caractères écrits à la main dans différentes classes, telles que les lettres de l'alphabet ou les chiffres.

Théorème de Bayes

• \(P(A), P(B)\) sont des probabilités d'observer A et B indépendamment l'un de l'autre.
• \(P(A|B)\) est une probabilité conditionnelle, la probabilité que l'événement \(A\) se produise étant donné que \(B\) est vrai
• \(P(B|A)\) est une probabilité conditionnelle, la probabilité que l'événement \(B\) se produise étant donné que \(A\) est vrai
• \(P(B) ≠ 0\)

\[P(A|B) = \frac{(P(B|A).P(A))}{P(B)}\]

Théorème de Bayes: Classification d'un message

• \(P(S)\) est la probabilité globale qu'un message donné soit un spam.
• \(P(H)\) est la probabilité globale qu'un message donné ne soit pas du spam.
• \(P(S|W)\) est la probabilité qu'un message soit un spam, sachant que le mot s'y trouve ;
• \(P(W|S)\) est la probabilité que le mot apparaisse dans les messages de spam ;
• \(P(W|H)\) est la probabilité que le mot "réplique" apparaisse dans les messages ham.

\[P(S|W) = \frac{P(W|S) \cdot P(S)}{P(W|S) \cdot P(S) + P(W|H) \cdot P(H)}\]

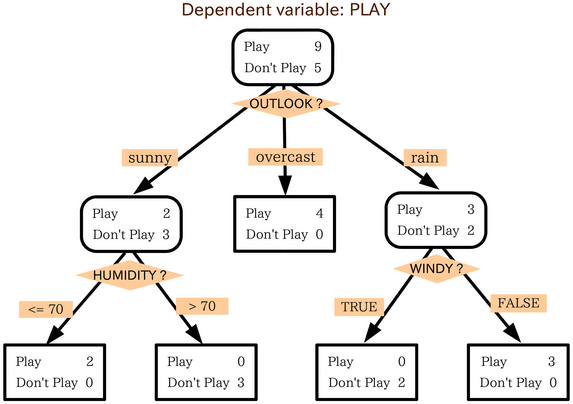
Les arbres de décision sont un outil puissant d'aide à la décision qui utilise un modèle arborescent pour représenter les décisions et leurs conséquences possibles

• Modèle arborescent : Les arbres de décision représentent les décisions sous forme d'un arbre, où chaque nœud interne représente une caractéristique (ou attribut), chaque branche représente une décision basée sur cette caractéristique, et chaque feuille représente un résultat ou une classe.
• Facile à interpréter : Les arbres de décision sont faciles à comprendre et à interpréter, ce qui les rend populaires pour la prise de décision dans de nombreux domaines.
• Adaptabilité : Ils peuvent être utilisés pour modéliser des problèmes de classification ainsi que des problèmes de régression.
• Utilisation de règles simples : Les décisions sont prises en suivant des règles simples basées sur les valeurs des caractéristiques, ce qui rend l'interprétation des résultats facile même pour les non-experts.

Nous voulons classer ces animaux en trois classes : Mammifère, Oiseau ou Reptile. Utilisons un arbre de décision pour ce faire.

L'algorithme de l'arbre de décision est une méthode d'apprentissage supervisé utilisée pour la classification et la régression.

• Choix de la caractéristique de division : L'algorithme commence par choisir la meilleure caractéristique pour diviser les données en sous-ensembles homogènes. Dans l'exemple, la première caractéristique choisie est le pelage.
• Division des données : Les données sont divisées en sous-groupes en fonction de la caractéristique choisie. Dans l'exemple, les données sont divisées en deux groupes : ceux avec un pelage poilu et ceux avec un pelage plumeux.
• Récursion : Le processus est répété de manière récursive pour chaque sous-groupe obtenu. Pour chaque sous-groupe, l'algorithme choisit à nouveau la meilleure caractéristique de division et divise les données en sous-groupes plus petits. Dans notre exemple, pour les animaux avec un pelage plumeux, la capacité de voler est la caractéristique de division suivante.

• Critère d'arrêt : L'algorithme s'arrête lorsque l'une des conditions suivantes est remplie :
  • Tous les éléments d'un sous-groupe appartiennent à la même classe.
  • Toutes les caractéristiques ont été utilisées pour la division.
  • Une profondeur maximale de l'arbre est atteinte.
  • Un nombre minimal d'échantillons dans un nœud est atteint.
• Construction de l'arbre : Une fois que les divisions sont terminées, un arbre de décision est construit où chaque nœud représente une caractéristique de division et chaque feuille représente une classe de sortie.
• Classification : Lorsqu'un nouvel exemple est introduit, il est classé en parcourant l'arbre de décision en fonction de ses caractéristiques jusqu'à atteindre une feuille, où il est attribué à une classe.

Dans le contexte des arbres de décision, les données sont généralement représentées sous forme de vecteurs où chaque élément du vecteur correspond à une caractéristique ou à une variable indépendante, et la variable dépendante est la cible que l'on cherche à prédire ou à classifier.

• Données sous forme de vecteurs : Chaque observation ou exemple dans l'ensemble de données est représenté sous forme d'un vecteur, où chaque composante du vecteur correspond à une caractéristique ou à une variable explicative. Par exemple, si nous examinons un ensemble de données sur les prêts bancaires, les caractéristiques pourraient inclure le revenu, le montant du prêt, le nombre d'années d'expérience professionnelle, etc.
• Les données sont disponibles sous la forme \[(\textbf{x},Y) = (x_1, x_2, x_3, ..., x_k, Y)\]
• Le vecteur \(\textbf{x}\) est composé des caractéristiques suivantes \(x_1, x_2, x_3, ...\)
• \(Y\) est la variable dépendante qui peut dépendre de \(\textbf{x}\)

Applications

• Classification : Les arbres de décision sont couramment utilisés pour la classification, où l'objectif est de catégoriser les observations dans des classes ou des catégories prédéfinies en fonction de leurs caractéristiques. Par exemple, dans le domaine médical, les arbres de décision peuvent être utilisés pour classifier les patients en fonction de leur diagnostic.
• Régression : Les arbres de décision peuvent également être utilisés pour la régression, où l'objectif est de prédire une valeur numérique continue en fonction des caractéristiques. Par exemple, dans les finances, les arbres de décision peuvent être utilisés pour prédire le prix d'une maison en fonction de ses caractéristiques.
• Analyse de la décision : Les arbres de décision peuvent aider à identifier les stratégies ou les séquences d'actions les plus efficaces pour atteindre un objectif spécifique. Par exemple, dans la planification d'entreprise, les arbres de décision peuvent être utilisés pour déterminer les meilleures décisions à prendre dans un processus de prise de décision complexe.

Applications

• Recherche opérationnelle : Les arbres de décision sont également utilisés dans le domaine de la recherche opérationnelle pour résoudre des problèmes d'optimisation et de planification. Par exemple, dans la logistique, les arbres de décision peuvent être utilisés pour déterminer le meilleur itinéraire de livraison en fonction de divers facteurs tels que la distance, le coût et les contraintes de temps.

L'apprentissage ensembliste, en particulier les forêts d'arbres décisionnels, est une technique qui combine plusieurs modèles d'apprentissage pour améliorer les performances prédictives par rapport à un seul modèle. Les forêts d'arbres décisionnels sont obtenues en construisant de multiples arbres de décision lors de la phase d'entraînement.

• Construction des arbres de décision : Pendant la phase d'entraînement, plusieurs arbres de décision sont construits en utilisant différents sous-ensembles de données et/ou caractéristiques. Chaque arbre est formé de manière indépendante.

• Vote majoritaire : Pour la classification, chaque arbre de décision vote pour la classe prédite d'un nouvel exemple. La classe finale attribuée à l'exemple est déterminée par un vote majoritaire parmi tous les arbres de la forêt. Pour la régression, les valeurs prédites par chaque arbre sont moyennées pour obtenir la valeur finale.
• Réduction de la variance : L'apprentissage ensembliste vise à réduire la variance du modèle en agrégeant plusieurs modèles. Cela peut aider à éviter le surajustement (overfitting) en compensant les défauts individuels de chaque arbre de décision.
• Stabilité : Les forêts d'arbres décisionnels sont généralement plus stables que les arbres de décision individuels, car elles sont moins sensibles aux variations des données d'entraînement.

Algorithme

• Soit \(X = x_1,x_2,..x_n\) un ensemble de données avec des réponses \(Y = y_1,y_2,..y_n\)
• Soit \(b = 1, 2,..B\)
  • Échantillon, avec remplacement (un élément peut apparaître plusieurs fois dans un même échantillon), \(n\) exemples de formation de \(X, Y\) ; appelez-les \(X_b, Y_b\).
  • Former un arbre de classification ou de régression \(f_b\) sur \(X_b, Y_b\).
• Après entraînement, les prédictions pour les échantillons non vus x' peuvent être faites en faisant la moyenne des prédictions de tous les arbres de régression individuels sur x' \[\hat{f} = \frac{1}{B} \sum_{b=1}^Bf_b (x')\] ou par un vote à la majorité dans le cas des arbres de classification.

Applications

• Classification multiclasse : les forêts d'arbres décisionnels sont utilisées pour classer les instances dans l'une des plusieurs classes mutuellement exclusives. Par exemple, la classification d'images en différentes catégories telles que les animaux, les véhicules, les objets ménagers, etc.
• Classification multilabel : Contrairement à la classification multiclasse, la classification multilabel permet qu'une instance soit assignée à plusieurs classes en même temps. Par exemple, la classification de documents dans lesquels un document peut être associé à plusieurs catégories telles que "science", "technologie", "politique", etc.

Applications

• Régression : les forêts d'arbres décisionnels peuvent également être utilisées pour des tâches de régression, où la sortie est une valeur continue plutôt qu'une classe discrète. Par exemple, prédire le prix d'une maison en fonction de ses caractéristiques.
• Détection des anomalies : Elles peuvent également être employées pour détecter les anomalies ou les comportements inhabituels dans les données. Cela peut être utile dans divers domaines tels que la détection de fraudes financières, la détection de défaillances dans les systèmes industriels, etc.

La sélection de caractéristiques est un processus visant à choisir un sous-ensemble de caractéristiques pertinentes parmi un grand nombre de caractéristiques disponibles.

• Cette technique est largement utilisée dans des domaines où le nombre de caractéristiques est élevé par rapport à la taille de l'échantillon de données, car cela peut entraîner des problèmes de surajustement et de temps de calcul élevé.
• La sélection de caractéristiques est également considérée comme une méthode de réduction de la dimensionnalité, car elle vise à réduire le nombre de dimensions de l'espace des caractéristiques sans perdre d'informations discriminatives.
• la sélection de caractéristiques vise à :
  • Identifier les caractéristiques les plus pertinentes qui contribuent le plus à la variabilité des données ou à la capacité de prédiction du modèle.
  • Réduire la dimensionnalité de l'espace des caractéristiques pour améliorer les performances des modèles d'apprentissage automatique en termes de temps de calcul et de prévention du surajustement.

Applications

• Analyse des textes écrits : Dans l'analyse de textes écrits, la sélection de caractéristiques est effectivement utilisée pour extraire les éléments les plus pertinents et informatifs des données textuelles. Cela peut inclure l'identification des mots clés, des entités nommées, des motifs linguistiques spécifiques ou d'autres caractéristiques qui sont essentielles pour la tâche d'analyse de texte, comme la classification de documents, l'extraction d'informations ou la génération de résumés. La sélection de caractéristiques dans ce contexte vise à réduire la dimensionnalité des données textuelles tout en préservant leur pertinence et leur expressivité pour les tâches d'analyse ultérieures.
• Analyse des données des puces à ADN : En génomique et bioinformatique, les puces à ADN génèrent des ensembles de données très dimensionnels qui nécessitent souvent une réduction de dimension pour identifier les gènes ou les séquences d'ADN les plus significatifs associés à des phénotypes particuliers, tels que des maladies ou des réponses biologiques.

Définition formelle[8]

• Soit \(X\) l'ensemble original de \(n\) caractéristiques, c'est-à-dire, \(|X| = n\)
• Soit \(w_i\) le poids attribué à l'élément \(x_i ∈ X\)
• La sélection binaire attribue des poids binaires tandis que la sélection continue attribue des poids en préservant l'ordre de sa pertinence.
• Soit \(J(X')\) soit une mesure d'évaluation, définie comme \(J: X' ⊆ X → R\)
• Le problème de la sélection des caractéristiques peut être défini de trois façons
  1. \(|X'| = m < n\). Trouver \(X' ⊂ X\) tel que \(J(X')\) est le maximum
  2. Choisir \(J_0\), Trouver \(X' ⊆ X\), tel que \(J(X') >= J_0\)
  3. Trouver un compromis entre la minimisation de \(|X'|\) et la maximisation du \(J(X')\)

Articles de recherche

1. From data mining to knowledge discovery in databases, Usama Fayyad, Gregory Piatetsky-Shapiro, and Padhraic Smyth, AI Magazine Volume 17 Number 3 (1996)
2. Survey of Clustering Data Mining Techniques, Pavel Berkhin
3. Mining association rules between sets of items in large databases, Agrawal, Rakesh, Tomasz Imieliński, and Arun Swami. Proceedings of the 1993 ACM SIGMOD international conference on Management of data - SIGMOD 1993. p. 207.
4. Comparisons of Sequence Labeling Algorithms and Extensions, Nguyen, Nam, and Yunsong Guo. Proceedings of the 24th international conference on Machine learning. ACM, 2007.

Articles de recherche

5. An Analysis of Active Learning Strategies for Sequence Labeling Tasks, Settles, Burr, and Mark Craven. Proceedings of the conference on empirical methods in natural language processing. Association for Computational Linguistics, 2008.
6. Anomaly detection in crowded scenes, Mahadevan; Vijay et al. Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. IEEE, 2010
7. A Study of Global Inference Algorithms in Multi-Document Summarization. McDonald, Ryan. European Conference on Information Retrieval. Springer, Berlin, Heidelberg, 2007.
8. Feature selection algorithms: A survey and experimental evaluation., Molina, Luis Carlos, Lluís Belanche, and Àngela Nebot. Data Mining, 2002. ICDM 2003. Proceedings. 2002 IEEE International Conference on. IEEE, 2002.
9. Support vector machines, Hearst, Marti A., et al. IEEE Intelligent Systems and their applications 13.4 (1998): 18-28.

Ressources en ligne

• Accuracy, Recall, Precision, F-Score & Specificity, which to optimize on?
• Patterns in Nature
• Data Mining
• Statistical classification
• Regression analysis
• Cluster analysis
• Association rule learning
• Anomaly detection

• Sequence labeling
• Automatic summarization
• Pattern recognition
• Scikit-learn

Ressources en ligne

• Support Vector Machines
• Decision tree learning
• Stochastic gradient descent

Couleurs

• Color Tool - Material Design

Images

• Wikimedia Commons