Apprentissage machine

John Samuel
CPE Lyon

Year: 2023-2024
Email: john(dot)samuel(at)cpe(dot)fr

Objectifs

1. Introduction à l'Intelligence Artificielle (IA)
2. Apprentissage Machine
3. Apprentissage Profond
4. Applications de l'IA

Devoir surveillé (DS): 60%

• Examen: En-ligne sur E-campus
• Durée: 2 heures
• Total: 10/20 points
• Documents: autorisés
• Types de documents autorisés: Tous les documents autorisés
• Calculatrices : non autorisées
• Utilisation de l'internet : non autorisée
• Dépôt supplémentaire : disponible pour les fichiers personnels

Vous recevrez un courrier détaillé avant l'examen

Travaux pratiques et Projet: 40%

• Les 2 travaux pratiques (TP) et le projet seront évalués.
• Deux dates limites de soumission sont précisées sur e-campus.

Cours	Nombre d'heures
Cours	16
TP	16
Projet	16

Attention : À chaque séance, nous adopterons un format intégrant à la fois des cours et des travaux pratiques.

Intelligence Artificielle [Pan 2016, Jaakkola 2019]

• La méthode d'apprentissage profond
• Les fusions et acquisitions d'entreprises
  • DNNresearch par Google en 2013 [1] : vision par ordinateur.
  • LinkedIn par Microsoft en 2016 [2] : réseaux sociaux professionnels.
• Les chatbots
  • Xiaobing par Microsoft: « comprendre » et répondre aux questions des utilisateurs en langage naturel.
• Les programmes de jeux
  • AlphaGo par Google : victoire historique contre le champion du jeu de go Lee Sedol en 2016.
• L'utilisation dans les hôpitaux
  • Watson par IBM : une plateforme d'IA qui a été utilisée dans le domaine de la santé pour aider les professionnels de la santé à analyser et à interpréter des données médicales complexes.
• La compréhension du langage naturel
  • Baidu : moteur de recherche.

Intelligence Artificielle [Pan 2016, Jaakkola 2019]

• 1956: la definition d'IA
  • La capacité des machines à comprendre, à penser et à apprendre d'une manière similaire à celle des êtres humains
  • Proposée par J. McCarthy, M. L. Minsky, H. Simon, A. Newell, C. E. Shannon, N. Rochester,...
• 1970-2000
  • 1983: le rapport par James Lighthill : un rapport critiquant la recherche en IA au Royaume-Uni, ce qui a conduit à un ralentissement temporaire des financements publics pour l'IA, connu sous le nom de « l'effet Lighthill ».
  • 1982-1992: l'échec du développement d'un ordinateur intelligent par le Japon
  • 1984: la construction manuelle d'une encyclopédie de la connaissance (Cyc) par Douglas Lenat à l'Université Stanford. Cyc est un projet d'IA visant à créer une base de connaissances informatisée capable de raisonner et de répondre à des questions complexes.

Intelligence Artificielle 2.0 [Pan 2016, Jaakkola 2019]

• 1990s-présent
  • Popularité de l'Internet
  • l'utilisation des capteurs
  • Big Data
  • l'e-commerce
• Des demandes sociales pour IA
  • des villes intelligentes
  • médecine
  • transport
  • les automobiles sans conducteur
  • les smartphones

Intelligence Artificielle 2.0 [Pan 2016]

• Les technologies à l'origine de l'IA
  • L'IA basée sur des données massives (Big Data)
  • L'intelligence de la foule sur Internet
  • Le savoir médiatique croisé
  • L'intelligence hybride homme-machine
  • Systèmes autonomes et intelligents
• L'avenir
  • L'IA explicative et générique
  • la cognition, l'apprentissage et l'inférence trans-médiatiques.
  • l'intelligence communautaire à partir de l'intelligence des foules basée sur l'intelligence individuelle
  • des systèmes autonomes et intelligents pour le développement de machines et de produits intelligents.

Objectifs

1.2. Les fondements de l'IA

• 1.2.1. Logique et raisonnement
• 1.2.2. Représentation des connaissances
• 1.2.3. Agents intelligents
• 1.2.4. Apprentissage machine
• 1.2.5. Apprentissage profond

Logique et raisonnement

• Logique propositionnelle : La logique propositionnelle est un système formel qui permet de représenter et d'évaluer des propositions en utilisant des connecteurs logiques (comme ET, OU, NON) pour déterminer leur vérité.
• Logique du premier ordre : La logique du premier ordre, également appelée logique des prédicats, est une extension de la logique propositionnelle qui permet de représenter des propositions plus complexes en introduisant des variables, des constantes, des fonctions et des prédicats.
• Logique modale : La logique modale est une extension de la logique qui permet de représenter des notions de possibilité, de nécessité, de croyance et d'autres modalités.
• Raisonnement automatisé : Le raisonnement automatisé fait référence à l'utilisation de systèmes informatiques pour effectuer des inférences logiques et déduire de nouvelles informations à partir de connaissances existantes.
• Problèmes de décision et résolution de problèmes : Les problèmes de décision se réfèrent à des situations où une décision doit être prise parmi plusieurs options possibles, généralement sous contraintes. La résolution de problèmes implique la recherche d'une solution à un problème donné en utilisant des méthodes algorithmiques ou heuristiques pour atteindre un objectif spécifique.

Logique propositionnelle

Les propositions dans la logique propositionnelle sont des déclarations qui peuvent être vraies (V) ou fausses (F). Supposons que nous ayons deux propositions simples : P, Q. Nous pouvons utiliser des connecteurs logiques pour créer des propositions plus complexes à partir de ces propositions simples.

• NON (¬) : La négation (NON) inverse la valeur de vérité d'une proposition. Si P est vrai, alors NON P est faux, et si P est faux, alors NON P est vrai.
• ET (ET logique, ∧) : L'opérateur ET (ou ET logique) est vrai seulement si toutes les propositions connectées par ET sont vraies. Si P est vrai et Q est vrai, alors P ET Q est vrai. Sinon, P ET Q est faux.
• OU (OU logique, ∨) : L'opérateur OU (ou OU logique) est vrai si au moins l'une des propositions connectées par OU est vraie. Si P est vrai ou Q est vrai (ou les deux), alors P OU Q est vrai. Si les deux sont faux, alors P OU Q est faux.

Logique propositionnelle

• Implication (=>) : L'implication (=>) exprime une relation où la vérité de la première proposition entraîne la vérité de la seconde. Si P est vrai, alors P => Q est vrai, peu importe la valeur de Q. Si P est faux, alors P => Q est toujours vrai, car il ne dit rien sur Q.
• Équivalence (<=>) : L'équivalence (<=>) signifie que deux propositions ont la même valeur de vérité dans toutes les situations. Si P est vrai et Q est vrai, ou si P est faux et Q est faux, alors P <=> Q est vrai. Sinon, c'est faux.

Logique propositionnelle

Supposons que nous ayons quatre propositions simples : P, Q, R et S.

• P : Présence de l'eau.
• Q : Présence de sable.
• R : Présence d'oiseaux marins.
• S : Présence de bateaux.

Logique propositionnelle

Avec ces propositions, nous pouvons définir des règles pour déterminer si une image représente la mer :

• Si l'eau est présente (P), alors il est possible que l'image soit celle de la mer.
• Si en plus il y a du sable (Q), cela renforce la probabilité que l'image soit une plage de mer.
• Si des oiseaux marins sont présents (R), cela renforce également la probabilité que la scène soit liée à la mer.
• Si des bateaux sont visibles (S), cela suggère une forte probabilité que la scène soit maritime.

nous pouvons utiliser des opérateurs logiques pour combiner ces propositions et déterminer si l'image est celle de la mer :

Image de la mer : (P ET Q) OU (P ET R) OU (P ET S)

Logique du premier ordre

Contrairement à la logique propositionnelle, qui traite uniquement de la vérité ou de la fausseté de propositions simples, la logique du premier ordre permet de représenter des informations structurées sur des objets et leurs relations. Voici quelques concepts clés de la logique du premier ordre :

• Variables : Les variables sont des symboles qui représentent des objets ou des éléments non spécifiés d'un domaine. Elles sont utilisées pour généraliser des expressions et représenter des objets de manière générique.
• Constantes : Les constantes sont des symboles qui représentent des objets spécifiques et immuables d'un domaine.
• Fonctions : Les fonctions sont des opérations qui prennent un ou plusieurs arguments et renvoient un résultat.

Utilisez des parenthèses pour indiquer la priorité des opérations et la structure de la formule.

Logique du premier ordre

• Prédicats : Les prédicats sont des expressions qui décrivent des relations entre des objets ou des propriétés de ces objets.
• Quantificateurs : Les quantificateurs, tels que "pour tout" (∀) et "il existe" (∃), sont utilisés pour spécifier la portée de variables dans une expression.
• Opérateurs logiques : Les opérateurs logiques tels que "ET" (∧), "OU" (∨), "NON" (¬), "Implication" (=>), et "Équivalence" (<=>) sont utilisés pour combiner des propositions et construire des formules plus complexes.

Utilisez des parenthèses pour indiquer la priorité des opérations et la structure de la formule.

Logique du premier ordre

Exemple :

• Variables : une variable pourrait être représentée par "x", où "x" peut représenter n'importe quelle mer.
• Constantes : des constantes pourraient être "Mer Méditerranée", "Mer Noire" et "Mer Rouge" pour représenter des mers spécifiques.
• Fonctions : Nous pourrions utiliser une fonction "Profondeur(x)" pour représenter la profondeur de la mer x. Par exemple, "Profondeur(Mer Méditerranée)" pourrait renvoyer la profondeur de la mer Méditerranée.

Logique du premier ordre

Exemple :

• Prédicats : Un prédicat tel que "Salée(x)" pourrait toujours être utilisé pour indiquer si une mer donnée (x) est salée ou non. Par exemple, "Salée(Mer Méditerranée)" serait vrai car la mer Méditerranée est salée..
• Quantificateurs : Les quantificateurs définissent la portée des variables dans une expression logique.
  • "∀x Salée(x)" signifierait que toutes les mers sont salées.
  • "∃x Superficie(x) > 100 000 km²" signifierait qu'il existe une mer dont la superficie est supérieure à 100 000 kilomètres carrés.

Les fonctions sont utilisées pour attribuer des valeurs à des objets ou effectuer des opérations, tandis que les prédicats sont utilisés pour exprimer des relations ou des propriétés entre des objets et renvoient une valeur booléenne indiquant si la relation est vraie ou non.

Logique du premier ordre

Utilisons l'exemple des règles pour confirmer qu'une image représente effectivement une mer.

• Constantes : Nos constantes pourraient être les noms d'images spécifiques ou d'autres identifiants uniques pour des images particulières.
• Variables : Nous pourrions utiliser une variable, disons "x", pour représenter une image générique.
• Prédicats : Les prédicats sont des expressions qui décrivent des relations entre des objets ou des propriétés de ces objets.
  • Un prédicat "ContientEau(x)" pourrait être utilisé pour indiquer si l'image x contient de l'eau.
  • Un prédicat "ContientSable(x)" pourrait être utilisé pour indiquer si l'image x contient du sable.
  • Un prédicat "ContientBateaux(x)" pourrait être utilisé pour indiquer si l'image x contient des bateaux.
  • Un prédicat "ContientOiseauxMarins(x)" pourrait être utilisé pour indiquer si l'image x contient des oiseaux marins.
• Quantificateurs : Nous pourrions utiliser des quantificateurs tels que "∃x" (il existe une image) ou "∀x" (pour toutes les images) pour spécifier la portée de nos règles.

Logique du premier ordre

1. Pour déterminer si une image représente une scène de mer, nous pourrions utiliser une règle du type

∀x (ContientEau(x) ∧ ContientSable(x) => EstMer(x))

2. Nous pourrions également ajouter des règles spécifiques pour détecter des éléments spécifiques :

∀x (ContientBateaux(x) => EstPort(x))

∀x (ContientOiseauxMarins(x) => EstPlage(x))

Logique du premier ordre

3. Il existe au moins une image x telle que l'image contienne de l'eau et du sable.

∃x (ContientEau(x) ∧ ContientSable(x))

Logique modale

La logique modale est une extension de la logique classique qui permet de raisonner sur la notion de "modalités", c'est-à-dire des catégories de propositions qui expriment des modalités ou des qualités spécifiques, telles que la nécessité, la possibilité, l'obligation, la croyance, etc

Opérateurs modaux : Les opérateurs modaux sont utilisés pour exprimer des modalités. Les deux opérateurs modaux les plus courants sont :

• ◻ (carré) : Il exprime la nécessité, indiquant que quelque chose est nécessairement vrai.
• ◇ (losange) : Il exprime la possibilité, indiquant que quelque chose est possible, mais pas nécessairement vrai.

Logique modale

En logique modale, les termes "nécessaire", "contingent", "possible" et "impossible" sont utilisés pour décrire les modalités ou les qualités d'une proposition.

• Nécessaire : Une proposition est dite "nécessaire" si elle est vraie dans toutes les situations possibles, c'est-à-dire qu'elle ne peut pas être fausse dans aucune situation imaginable. En notation modale, on utilise l'opérateur "◻" (carré) pour représenter la nécessité. Ainsi, "◻(P)" signifie "Il est nécessaire que P soit vrai."
• Contingent : Une proposition est dite "contingente" si elle est vraie dans certaines situations possibles et fausse dans d'autres. En d'autres termes, sa vérité dépend du contexte ou des conditions. Les propositions contingentes ne sont ni nécessairement vraies ni nécessairement fausses.

Logique modale

• Possible : Une proposition est dite "possible" si elle est vraie dans au moins une situation possible, même si elle n'est pas nécessairement vraie dans toutes les situations possibles. En notation modale, on utilise l'opérateur "◇" (losange) pour représenter la possibilité. Ainsi, "◇(Q)" signifie "Il est possible que Q soit vrai."
• Impossible : Une proposition est dite "impossible" si elle est fausse dans toutes les situations possibles, c'est-à-dire qu'elle ne peut pas être vraie dans aucune situation imaginable. En notation modale, l'opérateur de négation "¬" peut être utilisé en conjonction avec l'opérateur de possibilité "◇" pour représenter l'impossibilité. Ainsi, "¬◇(R)" signifie "Il est impossible que R soit vrai."

Logique modale

Exemple

• Nécessaire : "◻(Toute mer est salée)" signifie que dans toutes les situations possibles, toutes les mers sont salées.
• Contingent : "◇(Il peut y avoir des mers calmes)" signifie qu'il est possible d'avoir des mers calmes, mais elles ne sont pas nécessairement calmes dans toutes les situations possibles.
• Possible : : "◇(Il est possible qu'il y ait des tempêtes en mer)" signifie qu'il est possible qu'il y ait des tempêtes en mer, mais elles ne sont pas nécessaires dans toutes les situations possibles.
• Impossible : "¬◇(Toutes les mers sont douces)" signifie qu'il est impossible que toutes les mers soient douces.

Raisonnement automatisé

Le raisonnement automatisé est un domaine de l'intelligence artificielle (IA) qui concerne la création de systèmes informatiques capables de tirer des conclusions logiques et de résoudre des problèmes de manière autonome, similaire à la manière dont les humains utilisent leur raisonnement pour résoudre des problèmes.

• Objectif : L'objectif principal du raisonnement automatisé est de permettre aux machines de prendre des décisions, de résoudre des problèmes et de répondre à des questions en utilisant des règles logiques et des connaissances préalables.
• Inférence logique : Les moteurs d'inférence sont des composants logiciels qui appliquent des règles logiques et des axiomes pour déduire de nouvelles informations à partir des connaissances existantes. Cela implique souvent l'utilisation de la logique formelle, telle que la logique propositionnelle, la logique du premier ordre ou la logique modale.

Raisonnement automatisé

Le raisonnement automatisé peut être expliqué en utilisant différentes logiques, notamment la logique propositionnelle, la logique du premier ordre et la logique modale.

• Raisonnement automatisé en logique propositionnelle : Les connaissances sont représentées sous forme de propositions atomiques et de règles logiques qui décrivent comment ces propositions sont liées. Les moteurs d'inférence en logique propositionnelle appliquent des règles logiques pour tirer des conclusions à partir des propositions existantes.
• Raisonnement automatisé en logique du premier ordre logique : Les connaissances sont représentées de manière plus expressive, ce qui permet de modéliser des relations complexes entre objets et d'exprimer des généralisations. Les moteurs d'inférence en logique du premier ordre utilisent des règles de déduction plus sophistiquées, notamment l'utilisation de quantificateurs tels que "∀" (pour tout) et "∃" (il existe).
• Raisonnement automatisé en logique modale : : Les connaissances sont représentées avec des opérateurs modaux pour exprimer des propriétés modales, ce qui permet de traiter l'incertitude et la nécessité. Les moteurs d'inférence en logique modale utilisent des règles modales spécifiques pour tirer des conclusions en tenant compte des modalités.

Introduction

La représentation des connaissances joue un rôle central dans la manière dont les systèmes informatiques comprennent, raisonnent et interagissent avec le monde. La représentation des connaissances désigne le processus de capture, de structuration et de stockage des informations et des connaissances de manière à les rendre utilisables par des systèmes informatiques. Cela implique de transformer des données brutes ou des concepts en une forme que les ordinateurs peuvent comprendre et exploiter pour résoudre des problèmes, prendre des décisions ou interagir avec les utilisateurs.

• Résolution de Problèmes : Une représentation adéquate des connaissances permet aux systèmes informatiques de modéliser des problèmes complexes et de les résoudre de manière efficace. Elle facilite la manipulation et la déduction logique des informations pertinentes.
• Prise de Décisions Les machines doivent comprendre le monde qui les entoure pour interagir avec lui de manière significative. Une représentation des connaissances permet de modéliser des concepts tels que les objets, les relations, les événements et les règles.
• Communication Homme-Machine Lorsque des systèmes IA interagissent avec des utilisateurs humains, une représentation des connaissances claire et conviviale est essentielle pour rendre ces interactions compréhensibles et productives.

Types de connaissances

Les types de connaissances peuvent être classés en plusieurs catégories, notamment les connaissances déclaratives, les connaissances procédurales, les connaissances explicites et les connaissances tacites.

• Connaissances déclaratives : Les connaissances déclaratives se rapportent à "ce que nous savons". Elles sont constituées de faits, d'informations et de déclarations qui décrivent le monde ou une partie de celui-ci. Ces connaissances sont souvent exprimées sous forme de propositions ou de déclarations qui peuvent être vraies ou fausses.
• Connaissances procédurales Les connaissances procédurales concernent "comment faire quelque chose". Elles sont liées aux compétences, aux savoir-faire et aux procédures nécessaires pour accomplir des tâches ou des activités spécifiques. Ces connaissances sont généralement implicites et liées à l'expérience pratique.

Types de connaissances

• Connaissances explicites Les connaissances explicites sont des connaissances qui sont clairement exprimées et documentées. Elles sont généralement formelles et structurées de manière à être transmises et partagées facilement. Ces connaissances sont souvent consignées dans des manuels, des livres, des bases de données, ou d'autres formes de documentation.
• Connaissances tacites Les connaissances tacites sont des connaissances qui sont difficiles à exprimer verbalement ou à documenter de manière formelle. Elles résident souvent dans l'expérience personnelle, l'intuition, ou les compétences pratiques. Ces connaissances sont souvent difficiles à transférer d'une personne à une autre et sont souvent acquises par l'expérience.

Représentation des connaissances déclaratives

Dans la représentation des connaissances déclaratives, les faits, les informations et les connaissances sont exprimés sous forme de propositions logiques.

• Logique propositionnelle
• Logique du premier ordre

Représentation des connaissances déclaratives

Graphes de Connaissances (Ontologies): Les ontologies sont des structures de données hiérarchiques qui organisent et hiérarchisent les connaissances en utilisant des concepts, des classes, des propriétés et des relations.

• Concepts : Les ontologies définissent des concepts qui représentent des entités ou des idées du monde réel.
• Classes : Les concepts sont souvent organisés en classes.
• Propriétés : Les ontologies spécifient des propriétés et des relations entre les concepts.
• Relations : Les ontologies capturent les relations entre les concepts.

Introduction

Les agents intelligents sont des entités logicielles ou matérielles capables de percevoir leur environnement, de prendre des décisions, et d'agir pour atteindre des objectifs spécifiques. Un agent intelligent est un système informatique ou une entité physique qui possède certaines caractéristiques clés :

• Perception : Un agent intelligent est capable de percevoir son environnement à travers des capteurs ou d'autres moyens. Il collecte des informations sur l'état du monde qui l'entoure.
• Raisonnement : L'agent intelligent peut traiter les informations perçues, effectuer des calculs, et prendre des décisions basées sur ces données. Il peut utiliser des algorithmes, des méthodes d'apprentissage automatique, ou des règles de raisonnement formelles pour cela.
• Action : En réponse à ses décisions, l'agent intelligent peut agir sur son environnement en utilisant des actionneurs ou en émettant des commandes. Ses actions ont pour objectif d'atteindre des buts ou des objectifs spécifiques.
• Objectifs : Les agents intelligents sont souvent dotés d'objectifs ou de buts à atteindre. Ces objectifs définissent ce que l'agent tente d'accomplir dans son environnement.

Types d'agents intelligents

Les agents intelligents peuvent être classés en différents types en fonction de leurs caractéristiques et de leurs capacités.

• Agents réactifs simples : Les agents réactifs simples sont des agents intelligents qui réagissent directement aux stimuli de leur environnement sans avoir une représentation interne complexe du monde.
  • Ils prennent des décisions en se basant sur des règles préétablies qui associent des entrées (perceptions) à des sorties (actions).
  • Ces agents sont souvent utilisés pour des tâches spécifiques où la réactivité immédiate est cruciale, comme dans la robotique industrielle.
  • Cependant, ils ont tendance à manquer de capacité à anticiper ou à planifier des actions à long terme en l'absence de modèles internes complexes du monde.

Types d'agents intelligents

• Agents basés sur des modèles : Les agents basés sur des modèles utilisent une représentation interne du monde, généralement sous forme de modèles ou de cartes conceptuelles, pour comprendre leur environnement.
  • Ils utilisent ces modèles pour anticiper les conséquences de leurs actions, planifier des séquences d'actions et prendre des décisions éclairées.
  • Ces agents sont couramment utilisés dans des domaines tels que la planification automatisée, la simulation, et la modélisation de systèmes complexes.
  • Ils sont plus flexibles que les agents réactifs simples, mais leur performance dépend de la qualité de leurs modèles et de la capacité à anticiper les résultats.

Types d'agents intelligents

• Agents basés sur les buts : Les agents basés sur les buts ont des objectifs ou des buts à atteindre, et leur comportement est guidé par la poursuite de ces buts.
  • Ils évaluent régulièrement l'état de l'environnement et déterminent les actions à entreprendre pour se rapprocher de leurs objectifs.
  • Ces agents peuvent planifier et ajuster leurs actions en fonction de l'évolution de la situation pour maximiser leurs chances de succès. Ils sont couramment utilisés dans des domaines tels que la planification de parcours, les systèmes de recommandation, et les agents d'assistance personnelle.

Types d'agents intelligents

• Agents hybrides : Certains agents intelligents combinent des caractéristiques de plusieurs types d'agents pour tirer parti des avantages de chacun.
  • Par exemple, un agent hybride pourrait être réactif dans des situations immédiates, mais basé sur des modèles ou basé sur des buts pour des tâches plus complexes ou à long terme.
  • L'hybridation permet de créer des agents plus polyvalents capables de s'adapter à une variété de scénarios.

3 approches

1. Apprentissage supervisé:
   • Un modèle est formé à partir d'un ensemble de données de formation qui sont étiquetées, c'est-à-dire que chaque exemple de données est associé à une étiquette ou une catégorie connue.
   • L'objectif du modèle est d'apprendre à faire des prédictions en utilisant ces étiquettes de manière à pouvoir généraliser et faire des prédictions précises sur de nouvelles données non vues.
   • Par exemple, la classification d'images, la prédiction de prix, et la détection de spam dans les emails.
2. Apprentissage non supervisé:
   • Il n'y a pas de données de formation labellisées.
   • Le modèle doit découvrir des structures, des modèles ou des regroupements dans les données par lui-même.
   • Par exemple, la segmentation de clients en groupes, la réduction de la dimensionnalité, ou la détection d'anomalies.

3 approches

3. Apprentissage semi-supervisé:
   • Il repose sur un petit ensemble de données de formation étiquetées et une grande quantité de données non étiquetées.
   • Le modèle utilise les données étiquetées pour apprendre à faire des prédictions, mais il peut également tirer parti des données non étiquetées pour améliorer sa performance.
   • Cela peut être particulièrement utile lorsque l'obtention de données étiquetées est coûteuse ou difficile.

Apprentissage profond

Dans l'apprentissage profond, le terme profond fait référence à la présence de multiples couches dans le réseau neuronal. Contrairement aux modèles plus simples, tels que les perceptrons monocouche, les réseaux profonds ont la capacité d'apprendre des représentations hiérarchiques complexes à partir de données brutes.

• Perceptron linéaire et XOR : Un perceptron linéaire simple ne peut pas être un classificateur universel. Il est incapable de résoudre des problèmes non linéaires complexes, comme le problème XOR. Cependant, en ajoutant des couches et des non-linéarités (fonctions d'activation) aux perceptrons, on peut construire des réseaux neuronaux capables de résoudre des problèmes plus complexes.
• Extraction progressive de caractéristiques : Une caractéristique clé de l'apprentissage profond est la capacité à extraire progressivement des caractéristiques complexes à partir de données brutes. Chaque couche du réseau peut apprendre des représentations de plus en plus abstraites, permettant au modèle de comprendre des niveaux de complexité croissants dans les données.

L'apprentissage machine, également connu sous le nom de machine learning (ML), est un domaine de l'intelligence artificielle (IA) qui se concentre sur le développement de techniques permettant aux ordinateurs d'apprendre à partir de données. L'objectif principal de l'apprentissage machine est de permettre aux systèmes informatiques de prendre des décisions ou de réaliser des tâches sans être explicitement programmés, en s'appuyant sur des modèles et des motifs appris à partir des données.

Principes fondamentaux de l'apprentissage machine

• Données d'entraînement : L'apprentissage machine commence par des données. Ces données, appelées données d'entraînement, sont utilisées pour enseigner au modèle les modèles et les relations dans lesquels il doit identifier.
• Modèles : Les modèles en apprentissage machine sont des représentations mathématiques qui capturent les relations entre les différentes caractéristiques des données. Ces modèles sont entraînés à partir des données d'entraînement et sont capables de généraliser pour faire des prédictions sur de nouvelles données non vues.

Principes fondamentaux de l'apprentissage machine

• Entraînement et apprentissage : L'entraînement d'un modèle implique de l'exposer aux données d'entraînement, lui permettant d'ajuster ses paramètres pour minimiser les erreurs de prédiction. L'apprentissage se produit lorsque le modèle améliore sa capacité à faire des prédictions précises.
• Validation et test : Après l'entraînement, le modèle est évalué sur des données de validation et de test pour s'assurer qu'il généralise bien aux données non vues. Cela aide à éviter le surajustement, où le modèle apprend trop spécifiquement les données d'entraînement et ne peut pas généraliser correctement.

L'apprentissage machine occupe une place centrale dans le paysage technologique actuel et a un impact significatif dans divers domaines.

• Intelligence Artificielle (IA) : L'apprentissage machine est une composante essentielle de l'intelligence artificielle. Il permet aux systèmes informatiques de tirer des conclusions, d'apprendre à partir d'expériences passées et d'améliorer leur performance sans être explicitement programmés.
• Informatique et Technologie : L'apprentissage machine est largement utilisé dans les applications technologiques, y compris la vision par ordinateur, la reconnaissance vocale, la traduction automatique, les chatbots, et diverses autres applications qui exploitent la capacité des modèles à apprendre des données.
• Santé : Dans le domaine de la santé, l'apprentissage machine est utilisé pour la prédiction de maladies, l'analyse d'images médicales, la personnalisation des traitements, la découverte de médicaments, et la gestion des dossiers médicaux électroniques.
• Finance : Les institutions financières utilisent l'apprentissage machine pour la détection de fraudes, la prévision de tendances du marché, l'analyse de crédit, et l'optimisation des portefeuilles d'investissement.
• Industrie : Dans le secteur industriel, l'apprentissage machine est appliqué à la maintenance prédictive, à l'optimisation de la chaîne d'approvisionnement, à la qualité de production, et à la robotique.

Approches

• Apprentissage supervisé : Le modèle est entraîné sur un ensemble de données étiquetées où les exemples d'entrée sont associés à des sorties désirées. Le modèle apprend à faire des prédictions sur de nouvelles données en se basant sur ces associations.
• Apprentissage non supervisé : Le modèle est exposé à des données non étiquetées et cherche à découvrir des modèles, des structures ou des relations intrinsèques dans les données.
• Apprentissage semi-supervisé : Une combinaison des deux précédents, utilisant à la fois des données étiquetées et non étiquetées pour l'entraînement.
• Apprentissage par renforcement : Le modèle apprend à prendre des décisions en interagissant avec son environnement. Il reçoit des récompenses ou des pénalités en fonction de ses actions, ce qui guide son apprentissage.

Formalisation

• Vecteur euclidien:
  • Un vecteur euclidien est un objet géométrique caractérisé par sa magnitude (longueur) et sa direction.
  • Les vecteurs euclidiens sont couramment utilisés pour représenter des données sous forme de points dans un espace multidimensionnel, où chaque dimension correspond à une caractéristique ou une variable.
• Espace vectoriel:
  • Un espace vectoriel est une collection de vecteurs qui peuvent être additionnés entre eux et multipliés par des nombres (scalaires).
• Vecteur de caractéristiques (features):
  • Un vecteur de caractéristiques est un vecteur n-dimensionnel qui représente les caractéristiques ou les attributs d'une entité.
• Espace de caractéristiques:
  • L'espace de caractéristiques est l'espace vectoriel associé aux vecteurs de caractéristiques.
  • Chaque dimension de cet espace représente une caractéristique particulière, et les vecteurs sont utilisés pour positionner les données dans cet espace en fonction de leurs caractéristiques.

Exemples de caractéristiques

• Images: Dans le contexte des images, les vecteurs de caractéristiques peuvent être construits à partir des valeurs des pixels. Chaque pixel peut être considéré comme une dimension, et un vecteur de caractéristiques contiendra les valeurs de tous les pixels, permettant ainsi de représenter une image sous forme de vecteur.
• Textes: Pour les textes, les vecteurs de caractéristiques sont souvent construits à partir de la fréquence d'apparition des mots, des phrases, ou des tokens dans un document. Cela permet de représenter le contenu textuel en utilisant des valeurs numériques, ce qui est essentiel pour l'analyse de texte et la recherche d'informations.

Formalisation

• Construction de caractéristiques¹:
  • La construction de caractéristiques consiste à créer de nouvelles variables ou attributs à partir de celles déjà présentes dans les données.
  • Cette étape peut être cruciale pour améliorer les performances des modèles d'apprentissage machine en introduisant des informations pertinentes et en éliminant du bruit.
• Opérateurs de construction pour les caractéristiques
  • Les opérateurs de construction sont des fonctions ou des opérations mathématiques qui permettent de créer de nouvelles caractéristiques à partir de celles existantes.
  • Parmi les opérateurs couramment utilisés, on trouve les opérateurs d'égalité (comparaisons), les opérateurs arithmétiques (addition, soustraction, multiplication, division), les opérateurs de tableau (min, max, moyenne, médiane, etc.), les fonctions de transformation, etc.

1. https://en.wikipedia.org/wiki/Feature_vector

Exemple

• Soit Année de naissance et Année de décès deux caractéristiques existantes.
• Une nouvelle caractéristique appelée âge est créée. âge = Année de décès - Année de naissance

La construction de caractéristiques est une étape essentielle dans le pipeline de prétraitement des données en apprentissage machine, car elle peut aider à rendre les données plus informatives pour les algorithmes d'apprentissage.

Formalisation: Apprentissage supervisé

• Le nombre d'exemples d'entraînement (N) : Cela représente la quantité d'exemples de données que vous avez pour entraîner un modèle supervisé. Chaque exemple d'entraînement se compose d'un vecteur de caractéristiques (x) et de son label (y).
• L'espace de saisie des caractéristiques (X) : C'est l'ensemble de toutes les combinaisons possibles de vecteurs de caractéristiques qui peuvent être utilisées comme entrée pour le modèle. Cet espace est défini par les caractéristiques que vous avez extraites des données.
• L'espace des caractéristiques de sortie (Y) : Il représente l'ensemble de toutes les valeurs possibles que peuvent prendre les étiquettes ou les labels.
• Exemples d'entraînement (D) : C'est votre ensemble de données d'entraînement, composé de paires (x, y) où x est le vecteur de caractéristiques et y est le label correspondant.

Formalisation: Apprentissage supervisé

• Objectif de l'algorithme d'apprentissage supervisé : Il s'agit de trouver une fonction (g) qui associe un vecteur de caractéristiques (x) à un label (y). L'ensemble des fonctions possibles est appelé espace des hypothèses (G). L'objectif est de choisir la fonction (g) qui minimise l'erreur de prédiction sur les exemples d'entraînement et généralise bien sur de nouvelles données.
• Fonction d'évaluation (F) : Elle indique l'espace des fonctions d'évaluation utilisées pour évaluer la performance des fonctions hypothétiques. L'objectif est de trouver la fonction (g) qui renvoie la fonction d'évaluation (f) la plus élevée, c'est-à-dire celle qui donne les prédictions les plus précises.

Formalisation: Apprentissage supervisé

Cette formalisation est au cœur de l'apprentissage supervisé, où l'objectif est d'apprendre à partir d'exemples étiquetés et de trouver une fonction qui puisse prédire de manière précise les étiquettes pour de nouvelles données non vues.

• Soit \(N\) le nombre d'exemples d'entraînement
• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• Soit \({(x_1, y_1),...,(x_N, y_N)}\) les \(N\) exemples d'entraînement, où
  • \(x_i\) est le vecteur de caractéristiques de i^ème exemple d'entraînement.
  • \(y_i\) est son label.

Formalisation: Apprentissage supervisé

• L'objectif de l'algorithme d'apprentissage supervisé est de trouver \(g: X → Y\), où
  • g est l'une des fonctions de l'ensemble des fonctions possibles G (espace des hypothèses)
• Fonction d'évaluation F indiquent l'espace des fonctions d'évaluation, où
  • \(f: X × Y → R\) telle que g renvoie la fonction d'évaluation la plus élevée.

Formalisation: Apprentissage non supervisé

• L'espace de saisie des caractéristiques (X) : C'est l'ensemble de toutes les combinaisons possibles de vecteurs de caractéristiques qui peuvent être utilisées comme entrée pour le modèle en apprentissage non supervisé. Cet espace est défini par les caractéristiques que vous avez extraites des données.
• L'espace des caractéristiques de sortie (Y) : Il représente l'ensemble des caractéristiques de sortie potentielles. Contrairement à l'apprentissage supervisé, en apprentissage non supervisé, Y ne consiste pas en des étiquettes ou des labels prédéfinis, mais plutôt en des transformations, des représentations, ou des caractéristiques extraites des données d'entrée.
• Objectif de l'algorithme d'apprentissage non supervisé : L'objectif est de trouver une correspondance entre l'espace de saisie des caractéristiques (X) et l'espace des caractéristiques de sortie (Y). Cela peut impliquer diverses tâches, telles que la réduction de la dimensionnalité, la classification automatique de données non étiquetées, la détection d'anomalies, la segmentation, ou la représentation latente des données.
• Mise en correspondance X → Y : Cette mise en correspondance peut être réalisée de différentes manières, selon la tâche d'apprentissage non supervisé spécifique. Par exemple, dans la réduction de la dimensionnalité, X peut être une représentation à haute dimension des données, tandis que Y représente la version réduite de ces données, souvent avec moins de dimensions.

Formalisation: Apprentissage non supervisé

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• L'objectif de l'algorithme d'apprentissage non supervisé est
  • trouver la mise en correspondance \(X → Y\)

L'apprentissage non supervisé est utilisé pour explorer et découvrir des modèles, des structures ou des caractéristiques inhérentes aux données, sans l'utilisation d'étiquettes ou de labels préalables. Il est couramment utilisé dans des domaines tels que la clustering, l'analyse de composantes principales (PCA), l'analyse en composantes indépendantes (ICA), et bien d'autres.

Formalisation: Apprentissage semi-supervisé

• L'espace de saisie des caractéristiques (X) : Il s'agit de l'ensemble de toutes les combinaisons possibles de vecteurs de caractéristiques qui peuvent être utilisés comme entrée pour le modèle en apprentissage semi-supervisé.
• L'espace des caractéristiques de sortie (Y) : Il représente l'ensemble des caractéristiques de sortie potentielles, mais contrairement à l'apprentissage supervisé, il n'est pas nécessairement constitué d'étiquettes ou de labels prédéfinis.
• Ensemble d'exemples d'exercices étiquetés (l) : Cela correspond à un sous-ensemble d'exemples qui ont été annotés ou étiquetés avec des valeurs de sortie connues.
• Ensembles des vecteurs de caractéristiques non étiquetées (u) : Il s'agit des exemples non étiquetés, où les valeurs de sortie ne sont pas connues.

Formalisation: Apprentissage semi-supervisé

• Objectif de l'algorithme d'apprentissage semi-supervisé : L'objectif principal est de trouver des étiquettes correctes pour les exemples non étiquetés (apprentissage transductif), ainsi que de trouver la bonne mise en correspondance entre les caractéristiques d'entrée et les caractéristiques de sortie (apprentissage inductif).
  • Apprentissage transductif : Il s'agit de trouver des étiquettes correctes pour les exemples non étiquetés. Cela revient à prédire les valeurs de sortie pour les exemples non étiquetés sans nécessairement chercher à généraliser à de nouvelles données.
  • Apprentissage inductif : Cela concerne la recherche de la bonne mise en correspondance entre les vecteurs de caractéristiques d'entrée et les caractéristiques de sortie. Cela peut inclure la généralisation à de nouvelles données en utilisant le modèle appris.

Formalisation: Apprentissage semi-supervisé

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• Soit \({(x_1, y_1),...,(x_l, y_l)}\) l'ensemble d'exemples d'exercices étiquetés
• Soit \({x_{l+1},...,x_{l+u}}\) sont les \(u\) ensembles des vecteurs de caractéristiques non étiquetées de \(X\).
• L'objectif de l'algorithme d'apprentissage semi-supervisé est de faire
  • l'apprentissage transductif, c'est-à-dire trouver des étiquettes correctes pour \({x_{l+1},...,x_{l+u}}\).
  • l'apprentissage inductif, c'est-à-dire trouver la bonne mise en correspondance \(X → Y\)

Classification: Définition formelle

• Soit \(X\) l'espace de saisie des caractéristiques
• Soit \(Y\) l'espace des caractéristiques de sortie (des étiquettes)
• L'objectif de l'algorithme de classification (ou classificateur) est de trouver \({(x_1, y_1),...,(x_l, y_k)}\), c'est-à-dire l'attribution d'une étiquette connue à chaque vecteur de caractéristique d'entrée, où
  • \(x_i ∈ X \)
  • \(y_i ∈ Y \)
  • \(|X| = l \)
  • \(|Y| = k \)
  • \(l >= k\)

Classificateurs

• Algorithme de classification
• Deux types de classificateurs:
  • Classificateurs binaires attribue un objet à l'une des deux classes
  • Classificateurs multiclasses attribue un objet à une ou plusieurs classes

Classification binaire

Linear Classificateurs

• Fonction linéaire attribuant un score à chaque catégorie possible en combinant le vecteur de caractéristiques d'une instance avec un vecteur de poids, en utilisant un produit de points.
• Formalisation :
  • Soit X être l'espace de saisie des caractéristiques et x_i ∈ X
  • Soit β_k un vecteur de poids pour la catégorie k
  • score(x_i, k) = x_i.β_k, score pour l'attribution de la catégorie k à l'instance x_i. La catégorie qui donne le score le plus élevé est attribuée à la catégorie de l'instance.

Évaluation

Dans le contexte de la classification en apprentissage machine, l'évaluation des performances d'un modèle implique la compréhension de différents types de prédictions qu'il peut faire par rapport à la réalité. Les vrais positifs (VP) et les vrais négatifs (VN) sont deux de ces éléments.

• Vrais Positifs (VP/TP) : Les vrais positifs représentent les cas où le modèle prédit correctement la classe positive. En d'autres termes, il a correctement identifié les exemples qui appartiennent réellement à la classe que le modèle essaie de prédire.
• Vrais Négatifs (VN/FN) : Les vrais négatifs représentent les cas où le modèle prédit correctement la classe négative. Cela signifie qu'il a correctement identifié les exemples qui n'appartiennent pas à la classe que le modèle essaie de prédire.

Évaluation

Évaluation

Soit

• tp: nombre de vrais postifs
• fp: nombre de faux positifs
• fn: nombre de faux négatifs

Évaluation

La précision mesure la proportion de prédictions positives faites par le modèle qui étaient effectivement correctes, tandis que le rappel mesure la proportion d'exemples positifs réels qui ont été correctement identifiés par le modèle. Alors

• Précision \[p = \frac{tp}{(tp + fp)}\]
• Rappel (Recall) \[r = \frac{tp}{(tp + fn)}\]

Évaluation

Le F1-score est la moyenne harmonique de la précision et du rappel. Il fournit une mesure globale de la performance d'un modèle de classification, tenant compte à la fois de la précision et du rappel. Il est particulièrement utile lorsque les classes sont déséquilibrées.

• F1-score \[f1 = 2 * \frac{(p * r)}{(p + r)}\]
• F1-score: meilleure valeur à 1 (précision et rappel parfaits) et pire à 0.

Le F1-score tient compte à la fois des erreurs de type I (faux positifs) et des erreurs de type II (faux négatifs), fournissant ainsi une mesure équilibrée de la performance du modèle.

Évaluation

• \(F_\beta\)-score utilise un facteur réel positif β, où β est choisi de telle sorte que le rappel est considéré comme β fois plus important que la précision, est :
• \(F_\beta\)-score \[F_\beta = (1 + \beta^2) \cdot \frac{\mathrm{p} \cdot \mathrm{r}}{(\beta^2 \cdot \mathrm{p}) + \mathrm{r}}\]
• Exemple: \(F_2\) score: Cette métrique est souvent utilisée dans des situations où le rappel est jugé plus critique que la précision, par exemple, dans des tâches où la détection des exemples positifs est particulièrement importante, même si cela entraîne un nombre plus élevé de faux positifs.

Le \(F_2\)-score est souvent utilisé dans des domaines où le rappel est considéré comme plus critique que la précision.

• Détection de Maladies : Dans le domaine médical, en particulier pour la détection de maladies graves, le F2-score peut être utilisé pour évaluer la performance des modèles. Il est crucial d'identifier correctement autant de cas positifs que possible, même si cela conduit à quelques faux positifs.
• Sécurité et Détection d'Intrusion : Lors de la détection d'intrusions dans les systèmes informatiques, il est souvent plus important de minimiser les faux négatifs (intrusions manquées) au profit de quelques faux positifs, d'où l'utilisation du F2-score.
• Recherche Biomédicale : Dans des domaines de recherche biomédicale où la découverte de certaines caractéristiques ou protéines spécifiques est critique, le F2-score peut être privilégié pour s'assurer que ces éléments sont correctement identifiés.
• Prévision de Catastrophes Naturelles : Lors de la prévision de catastrophes naturelles comme les tremblements de terre ou les tsunamis, il est essentiel de minimiser les faux négatifs pour garantir que le maximum d'avertissements est donné, même au prix de quelques alertes erronées.
• Recherche en Astronomie : Dans la recherche astronomique, la découverte de nouveaux objets célestes ou de phénomènes rares peut être cruciale. Le F2-score peut être utilisé pour évaluer les performances des algorithmes de détection.

Évaluation: matrice de confusion

La matrice de confusion est un outil essentiel dans l'évaluation des performances d'un système de classification. Elle fournit une vue détaillée des prédictions faites par le modèle par rapport aux classes réelles.

• Chaque ligne de la matrice représente les instances d'une classe prédite.
• Chaque colonne représente les instances d'une classe réelle.
• Toutes les prédictions correctes sont situées dans la diagonale du tableau.
• Les erreurs de prédiction sont représentées par des valeurs situées en dehors de la diagonale principale.

Évaluation: matrice de confusion

Évaluation: matrice de confusion

Classification multiclasse

Classification multiclasse [Aly 2005]

• Transformation en classification binaire
  • L'approche un contre le reste (Un contre tous)
  • L'approche un-contre-un
• Extension de la classification binaire
  • Réseaux de neurones
  • k-voisins les plus proches
• la classification hiérarchique.

Classification multiclasse

Classification multiclasse

One-vs.-rest (One-vs.-all) strategy

Classification multiclasse

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

• Entraîner un seul classificateur par classe, avec les échantillons de cette classe comme échantillons positifs et tous les autres comme négatifs.
• Chaque classificateur produit un score de confiance réel pour sa décision

Classification multiclasse

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

• Entrées :
  • \(L\), un apprenant (algorithme d'entraînement pour les classificateurs binaires)
  • échantillons \(X\)
  • étiquettes \(y\), où \(y_i ∈ \{1,..,K \} \) est l'étiquette de l'échantillon \(X_i\)
• Sortie :
  • une liste de classificateurs \(f_k\), où \(k ∈ \{1,..,K \} \)

Classification multiclasse

One-vs.-rest or One-vs.-all (OvR, OvA) strategy

Prendre des décisions signifie appliquer tous les classificateurs à un échantillon invisible x et prédire l'étiquette k pour laquelle le classificateur correspondant rapporte le score de confiance le plus élevé : \[\hat{y} = \underset{k \in \{1 \ldots K\}}{\arg\!\max}\; f_k(x)\]

Classification multiclasse

One-vs.-one strategy

Classification multiclasse

One-vs.-one strategy

nécessite l'entraînement des \(\frac{K (K - 1)}{2}\) classificateurs binaires

chaque classificateur reçoit les échantillons d'une paire de classes du jeu de formation original, et doit apprendre à distinguer ces deux classes.

Au moment de la prédiction, un système de vote est appliqué : tous les \(\frac{K (K - 1)}{2}\) classificateurs sont appliqués à un échantillon non vu et la classe qui a obtenu le plus grand nombre de prédictions est prédite par le classificateur combiné.

Neurones biologiques

1. https://en.wikipedia.org/wiki/File:Neuron3.png

Introduction

Réseau de neurones

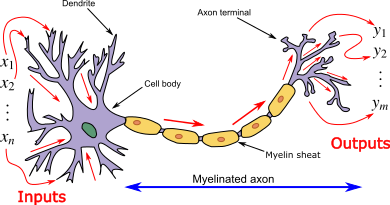
Les réseaux de neurones sont couramment utilisés dans le domaine de l'apprentissage machine, en particulier dans des tâches telles que la classification, la régression, la reconnaissance d'images, le traitement du langage naturel, et bien d'autres. Un réseau de neurones artificiels est une collection d'unités interconnectées appelées neurones artificiels. Ces réseaux sont inspirés de la structure du cerveau biologique

• Connexions : Chaque connexion entre les neurones, similaire aux synapses dans le cerveau biologique, peut transmettre un signal aux autres neurones.
• Transmission de signal : Un neurone artificiel reçoit un signal, le traite à l'aide d'une fonction non linéaire, et peut ensuite transmettre un signal aux neurones qui lui sont connectés.
• Fonction d'activation : La sortie de chaque neurone est calculée par une fonction non linéaire appliquée à la somme pondérée de ses entrées. Cette fonction d'activation introduit une non-linéarité dans le réseau, permettant de modéliser des relations complexes.

Réseau de neurones

• Poids ajustables : Les neurones et les connexions ont généralement des poids qui sont ajustés au fur et à mesure de l'apprentissage. Ces poids déterminent l'importance relative des différentes entrées pour chaque neurone.
• Ajustement des poids : Les poids peuvent être ajustés pour augmenter ou diminuer la force du signal au niveau d'une connexion, influençant ainsi la contribution de cette connexion aux calculs du réseau.
• Seuil : Les neurones peuvent avoir un seuil, de sorte qu'un signal n'est envoyé que si la somme pondérée de ses entrées dépasse ce seuil. Cela permet au réseau de moduler sa sensibilité aux entrées.

Les couches

Les neurones sont organisés en couches. Il existe généralement trois types de couches dans un réseau de neurones :

• Couche d'Entrée (Input Layer) : Cette couche reçoit les signaux initiaux ou les données en entrée. Chaque neurone dans cette couche représente une caractéristique ou une variable d'entrée.
• Couches Cachées (Hidden Layers) : Ces couches effectuent des transformations non linéaires sur les entrées. Elles sont responsables de l'extraction et de la représentation des caractéristiques importantes des données. Un réseau de neurones peut avoir une ou plusieurs couches cachées.
• Couche de Sortie (Output Layer) : Cette couche génère la sortie du réseau. Le nombre de neurones dans cette couche dépend de la nature de la tâche, par exemple, une classification binaire aurait un neurone de sortie, tandis qu'une classification multi-classes en aurait plusieurs.

Les couches

• Transformations : Chaque couche, y compris la couche d'entrée, effectue des transformations sur les signaux qu'elle reçoit. Ces transformations sont déterminées par les poids des connexions entre les neurones.
• Propagation des signaux : Les signaux passent de la première couche (l'entrée) à la dernière couche (la sortie) à travers les connexions pondérées entre les neurones. Ce processus est souvent appelé la propagation avant (forward propagation). Pendant l'apprentissage, la rétropropagation (backpropagation) est utilisée pour ajuster les poids afin de minimiser l'erreur de prédiction.
• Architecture : La manière dont les couches sont organisées et connectées dans le réseau constitue son architecture. Les réseaux de neurones peuvent avoir des architectures diverses, y compris des réseaux profonds (avec de nombreuses couches cachées) ou des architectures plus simples.

L'entraînement

L'objectif global de l'entraînement est d'ajuster les poids du réseau de manière à ce qu'il puisse généraliser à de nouvelles données, produisant des résultats précis pour des exemples qu'il n'a pas vu pendant l'entraînement.

• Données d'entraînement : Les réseaux neuronaux apprennent à partir d'exemples. Chaque exemple se compose d'une "entrée" (les caractéristiques) et d'un "résultat" connu (l'étiquette ou la sortie attendue).
• Calcul de l'erreur : Lorsque le réseau produit une sortie pour une entrée donnée, l'erreur est calculée en comparant cette sortie à la sortie cible (le résultat connu). Il existe différentes mesures d'erreur, mais la somme des carrés des différences (Mean Squared Error, MSE) est couramment utilisée.
• Rétropropagation (Backpropagation) : Le réseau ajuste ses poids en utilisant la rétropropagation. Cette technique minimise l'erreur en modifiant les poids à partir de la couche de sortie jusqu'à la couche d'entrée. La règle de la chaîne du calcul différentiel est appliquée pour propager l'erreur à travers le réseau.

L'entraînement

• Descente de gradient : La règle d'apprentissage souvent utilisée pour ajuster les poids est la descente de gradient. Elle utilise le gradient de l'erreur par rapport aux poids pour mettre à jour les poids dans la direction qui minimise l'erreur.
• Itérations : Le processus d'ajustement des poids en fonction de l'erreur est répété pour de nombreux exemples du jeu de données d'entraînement. Chaque itération est appelée une "époque". Plusieurs époques peuvent être nécessaires pour que le réseau converge vers un état où l'erreur est suffisamment basse.
• Optimisation : Différentes techniques d'optimisation peuvent être utilisées pour améliorer la convergence du réseau, telles que l'ajustement adaptatif du taux d'apprentissage.

Composants des réseaux de neurones artificiels

• Neurones : Les neurones artificiels sont les unités de base d'un réseau de neurones. Chaque neurone reçoit des signaux d'entrée, effectue un calcul sur ces signaux à l'aide d'une fonction d'activation, et produit une sortie. Les neurones sont organisés en couches, à savoir la couche d'entrée, les couches cachées, et la couche de sortie.
• Connexions et Poids : Les connexions entre les neurones sont représentées par des poids. Chaque connexion a un poids associé, qui détermine l'importance relative de cette connexion dans le calcul du neurone de sortie. Pendant l'entraînement, ces poids sont ajustés pour minimiser l'erreur de prédiction du réseau.
• Fonction de Propagation (Propagation avant) : La fonction de propagation, également appelée propagation avant, décrit le processus par lequel les signaux se propagent à travers le réseau depuis la couche d'entrée jusqu'à la couche de sortie. Chaque neurone effectue une transformation sur les signaux qu'il reçoit, et ces signaux modifiés sont transmis aux neurones de la couche suivante.

Composants des réseaux de neurones artificiels

Neurones

Chaque neurone artificiel a des entrées, qui peuvent être les valeurs caractéristiques d'un échantillon de données externe, et produit une seule sortie. Cette sortie peut être envoyée à plusieurs autres neurones, formant ainsi la structure interconnectée du réseau neuronal. La fonction d'activation joue un rôle crucial dans le calcul de la sortie d'un neurone. Le processus comprend les étapes suivantes :

• Somme pondérée : Pour trouver la sortie du neurone, on prend la somme pondérée de tous les intrants (entrées). Chaque entrée est multipliée par le poids correspondant à la connexion.
• Ajout d'un terme de biais : Un terme de biais est ajouté à la somme pondérée. Le terme de biais est un paramètre supplémentaire qui permet au modèle d'apprendre un décalage ou une translation.
• Activation : La somme pondérée, parfois appelée activation, est ensuite passée par une fonction d'activation. Cette fonction est généralement non linéaire et introduit de la complexité dans le modèle, permettant au réseau de capturer des relations non linéaires dans les données

Composants des réseaux de neurones artificiels

Connexions et poids

Le réseau de neurones est constitué de connexions, où chaque connexion transmet la sortie d'un neurone comme entrée à un autre neurone. Chaque connexion possède un poids qui représente son importance relative dans la transmission du signal.

• Un neurone donné peut avoir plusieurs connexions d'entrée, recevant des signaux de différents neurones, et plusieurs connexions de sortie, transmettant des signaux à d'autres neurones. Les poids associés à ces connexions permettent au réseau de moduler l'influence de chaque neurone sur les autres, ajustant ainsi la force et la direction des signaux transmis à travers le réseau.
• Cette structure de connexion et de pondération est fondamentale dans le fonctionnement des réseaux de neurones, car elle permet au réseau d'apprendre des représentations complexes des données et d'ajuster ses paramètres pendant l'entraînement pour accomplir des tâches spécifiques.

Composants des réseaux de neurones artificiels

Fonction de propagation

Calcul de l'entrée d'un neurone : La fonction de propagation calcule l'entrée d'un neurone en prenant la somme pondérée des sorties de ses prédécesseurs, où chaque sortie est multipliée par le poids de la connexion correspondante. Cela peut être représenté mathématiquement comme suit :

\[ \text{Entrée du Neurone} = \sum_{i=1}^{n} (\text{Sortie du Prédécesseur}_i \times \text{Poids}_i) \] où \(n\) est le nombre de connexions d'entrée.

Composants des réseaux de neurones artificiels

Fonction de propagation

Ajout d'un terme de biais : Un terme de biais peut être ajouté au résultat de la propagation. Le terme de biais est un paramètre supplémentaire, souvent représenté par \(b\) dans les équations, qui permet au modèle d'apprendre un décalage ou une translation. Cela donne la forme finale de l'entrée du neurone :

\[ \text{Entrée du Neurone} = \sum_{i=1}^{n} (\text{Sortie du Prédécesseur}_i \times \text{Poids}_i) + \text{Biais} \]

Composants des réseaux de neurones artificiels

Fonction de propagation

Fonction d'Activation : Après avoir calculé l'entrée du neurone, celle-ci est passée à travers une fonction d'activation. Cette fonction introduit une non-linéarité dans le modèle, permettant au réseau de neurones de capturer des relations complexes et d'apprendre des modèles non linéaires. Certaines des fonctions d'activation couramment utilisées comprennent :

• Sigmoïde : \( \sigma(x) = \frac{1}{1 + e^{-x}} \)
• Tangente hyperbolique (tanh) : \( \text{tanh}(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} \)
• ReLU (Rectified Linear Unit) : \( \text{ReLU}(x) = \max(0, x) \)
• Softmax (pour la couche de sortie dans la classification) : \( \text{Softmax}(x)_i = \frac{e^{x_i}}{\sum_{j} e^{x_j}} \)

Perceptron

Le perceptron est un algorithme d'apprentissage supervisé utilisé pour la classification binaire. Il est conçu pour résoudre des problèmes où l'objectif est de déterminer si une entrée donnée appartient ou non à une classe particulière.

• Le perceptron a été inventé par Frank Rosenblatt en 1958. L'idée était de créer un modèle simple de neurone artificiel inspiré du fonctionnement des neurones biologiques. Rosenblatt a formulé un algorithme d'apprentissage qui permet au perceptron d'ajuster ses poids en fonction des erreurs de classification, améliorant ainsi ses performances au fil du temps.
• Fonctionnement : Le perceptron prend plusieurs entrées pondérées et les combine en une somme. Ensuite, cette somme est soumise à une fonction d'activation, généralement une fonction échelon (step function), qui produit la sortie binaire du perceptron.
• Limitations : Le perceptron a des limitations, notamment sa capacité à résoudre des problèmes non linéaires et son incapacité à apprendre des modèles complexes. Cependant, il a jeté les bases pour le développement de réseaux de neurones plus avancés, en particulier les réseaux multicouches qui peuvent apprendre des représentations hiérarchiques.

Perceptron

1. Source: https://en.wikipedia.org/wiki/File:Perceptron_example.svg

Perceptron

Perceptron: Définition formelle

• Soit \(y = f(z)\) la sortie du perceptron pour un vecteur d'entrée z
• Soit \(N\) le nombre d'exemples d'entraînement
• Soit X l'espace de saisie des caractéristiques
• Soit \({(x_{1}, d_{1}),...,(x_{N}, d_{N})}\) be the N training examples, where
  • \(x_i\) est le vecteur caractéristique de i^ème exemple d'entraînement.
  • \(d_i\) est la valeur de sortie souhaitée
  • \(x_{j,i}\) est la i^ème caractéristique de j^ème exemple d'entraînement.
  • \(x_{j,0} = 1\)

Perceptron: Définition formelle

• Les poids sont représentés de la manière suivante:
  • \(w_i\) est la i^ème valeur du vecteur de poids.
  • \(w_i(t)\) est la i^ème valeur du vecteur de poids à un moment donné t.

Perceptron : Étapes

1. Initialiser les poids et les seuils
2. Pour chaque exemple, \((x_j, d_j)\) dans l'ensemble d'entraînement
   • Calculer la sortie actuelle : \[y_j(t)= f[w(t).x_j]\] \[= f[w_0(t)x_{j,0} + w_1(t)x_{j,1} + w_2(t)x_{j,2} + \dotsb + w_n(t)x_{j,n}]\]
   • Calculer le poids: \[w_i(t + 1) = w_i(t) + r. (d_j-y_j(t))x_{j,i}\]
   \(r\) est le taux d'apprentissage.

Perceptron : Étapes

3. Répétez l'étape 2 jusqu'à l'erreur d'itération \[\frac{1}{s} (Σ |d_j - y_j(t)|)\] est inférieur au seuil spécifié par l'utilisateur \(\gamma\), ou un nombre prédéterminé d'itérations ont été effectuées, où \(s\) est à nouveau la taille de l'ensemble de l'échantillon.

Fonction d'Échelon (Step Function)

Le perceptron utilise généralement une fonction d'activation simple, et la fonction d'échelon (step function) est fréquemment choisie pour cette tâche.

Définition

La fonction d'échelon attribue une sortie de 1 si la somme pondérée des entrées dépasse un certain seuil, et 0 sinon.

\( f(x) = \begin{cases} 1 & \text{si } x \geq \text{seuil} \\ 0 & \text{sinon} \end{cases} \)

Fonction d'activation: fonction d'identité

Équation

\[f(x)=x\]

Dérivée

\[f'(x)=1\]

Fonction d'activation: pas binaire

Équation

\[f(x) = \begin{cases} 0 & \text{for } x < 0\\ 1 & \text{for } x \ge 0 \end{cases} \]

Dérivée

\[f'(x) = \begin{cases} 0 & \text{for } x \ne 0\\ ? & \text{for } x = 0\end{cases}\]

Fonction d'activation: fonction sigmoïde

Équation

\[f(x)=\sigma(x)=\frac{1}{1+e^{-x}}\]

Dérivée

\[f'(x)=f(x)(1-f(x))\]

Fonction d'activation: TanH

Équation

\[f(x)=\tanh(x)=\frac{(e^{x} - e^{-x})}{(e^{x} + e^{-x})}\]

Dérivée

\[f'(x)=1-f(x)^2\]

Fonction d'activation: Rectified linear unit: ReLU

Équation

\[f(x) = \begin{cases} 0 & \text{for } x \le 0\\ x & \text{for } x > 0\end{cases} = \max\{0,x\}= x \textbf{1}_{x>0}\]

Dérivée

\[f'(x) = \begin{cases} 0 & \text{for } x \le 0\\ 1 & \text{for } x > 0\end{cases}\]

Fonction d'activation: Gaussien

Équation

\[f(x)=e^{-x^2}\]

Dérivée

\[f'(x)=-2xe^{-x^2}\]

Perceptron multiclasse

• Perceptron peut être généralisé à la classification multiclasse.
• Une fonction de représentation d'élément \(f( x , y )\) fait correspondre chaque paire d'entrée/sortie possible à un vecteur d'élément à valeur réelle en dimension finie.
• le vecteur de caractéristique est multiplié par un vecteur de poids \(w\), mais le score obtenu est maintenant utilisé pour choisir parmi de nombreux résultats possibles : \[\hat y = \operatorname{argmax}_y f(x,y) \cdot w.\]
• La réapprentissage se fait par itération sur les exemples, en prédisant un résultat pour chacun, en laissant les poids inchangés lorsque le résultat prédit correspond à l'objectif, et en les modifiant lorsqu'il ne correspond pas. La mise à jour devient : \[w_{t+1} = w_t + f(x, y) - f(x,\hat y)\].

Un réseau de neurones profond, également connu sous le nom de réseau de neurones profondément hiérarchisé ou réseau neuronal profond (DNN pour Deep Neural Network en anglais), est un type de réseau de neurones artificiels qui comprend plusieurs couches de traitement, généralement plus de deux. Ces réseaux sont appelés "profonds" en raison de leur architecture empilée de couches, permettant la création de représentations hiérarchiques complexes des données.

Architecture en couches : Les réseaux de neurones profonds sont composés de multiples couches, généralement divisées en trois types principaux :

• Couche d'Entrée : Reçoit les données brutes ou caractéristiques en entrée.
• Couches Cachées : Effectuent des transformations non linéaires et apprennent des représentations hiérarchiques des données.
• Couche de Sortie : Produit la sortie du réseau, adaptée à la tâche spécifique (classification, régression, etc.).

• Apprentissage Hiérarchique : Les couches cachées d'un réseau de neurones profond apprennent des caractéristiques de plus en plus abstraites et complexes à mesure que l'on progresse en profondeur. Chaque couche représente une abstraction des caractéristiques extraites par les couches précédentes.
• Fonctions d'Activation : Des fonctions d'activation non linéaires, telles que ReLU (Rectified Linear Unit) ou ses variantes, sont couramment utilisées dans les couches cachées pour permettre au réseau d'apprendre des relations non linéaires.
• Apprentissage Profond : L'apprentissage profond implique l'ajustement simultané des poids de toutes les couches du réseau pour minimiser l'erreur de prédiction. Cela est généralement réalisé en utilisant des techniques de rétropropagation et de descente de gradient.
• Utilisations : Les réseaux de neurones profonds sont utilisés dans une variété de tâches, notamment la vision par ordinateur, la reconnaissance vocale, le traitement du langage naturel, la traduction automatique, la recommandation de contenu, et bien d'autres. Leur capacité à apprendre des représentations complexes a conduit à des avancées significatives dans de nombreux domaines de l'intelligence artificielle.

L'entraînement de réseaux de neurones profonds peut nécessiter des volumes importants de données et de puissance de calcul.

Il existe plusieurs types de réseaux de neurones profonds.

• Réseaux de Neurones Convolutionnels (CNN) :
  • Utilisation Principale : Vision par ordinateur, reconnaissance d'images.
  • Caractéristiques : Les CNN sont efficaces pour extraire des motifs spatiaux à partir d'images en utilisant des opérations de convolution. Ils sont largement utilisés dans des applications telles que la classification d'images, la détection d'objets et la segmentation d'images.
• Réseaux de Neurones Récurrents (RNN) :
  • Utilisation Principale : Traitement de séquences, traitement du langage naturel.
  • Caractéristiques : Les RNN sont conçus pour traiter des données séquentielles en utilisant des connexions récurrentes qui leur permettent de conserver une mémoire à long terme. Ils sont utilisés pour des tâches telles que la traduction automatique, la génération de texte et l'analyse de séquences temporelles.

• Réseaux de Neurones Générateurs Adverses (GAN) :
  • Utilisation Principale : Génération d'images réalistes.
  • Caractéristiques : Les GAN sont composés de deux réseaux, un générateur et un discriminateur, qui s'entraînent de manière adversaire. Les GAN sont utilisés pour générer des données réalistes, y compris des images, des vidéos et du son.
• Réseaux de Neurones Résiduels (ResNet) :
  • Utilisation Principale : Classification d'images profondes.
  • Caractéristiques : Les architectures ResNet utilisent des connexions résiduelles pour faciliter l'apprentissage profond en surmontant le problème du "vanishing gradient". Ils sont fréquemment utilisés dans des compétitions de classification d'images.

• Autoencodeurs et Variational Autoencoders (VAE) :
  • Utilisation Principale : Compression et génération de données.
  • Caractéristiques : Les autoencodeurs sont utilisés pour apprendre des représentations compactes de données en comprimant et en reconstruisant les informations. Les VAE introduisent des composants probabilistes, permettant de générer de nouvelles données similaires aux données d'entraînement.
• Réseaux de Neurones de Mémoire à Long Terme (LSTM) :
  • Utilisation Principale : Traitement du langage naturel, séquences temporelles.
  • Caractéristiques : Les LSTMs sont une variation des RNN qui intègrent des mécanismes de portes pour mieux gérer le problème du gradient qui s'estompe sur de longues séquences. Ils sont couramment utilisés dans la génération de texte et d'autres tâches basées sur des séquences.

Articles de recherche

• [Aly 2005] Aly, Mohamed. Survey on Multiclass Classification Methods. 2005.
• [Jaakkola 2019] Jaakkola, H., et al. “Artificial Intelligence Yesterday, Today and Tomorrow.” 2019 42nd International Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), 2019, pp. 860–67. IEEE Xplore
• [Pan 2016] Pan, Yunhe, “Heading toward Artificial Intelligence 2.0.” Engineering, vol. 2, no. 4, Dec. 2016, pp. 409–13. www.sciencedirect.com,

Web

1. Google acquiert DNNresearch, spécialisé dans les réseaux de neurones profonds: https://www.lemondeinformatique.fr/actualites/lire-google-acquiert-dnnresearch-specialise-dans-les-reseaux-de-neurones-profonds-52829.html
2. Pourquoi Microsoft rachète Linkedin: https://www.lemondeinformatique.fr/actualites/lire-pourquoi-microsoft-rachete-linkedin-65136.html
3. Scikit-learn: http://scikit-learn.org/stable/
4. Perceptron: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.Perceptron.html

Wikipédia

• Perceptron: https://en.wikipedia.org/wiki/Perceptron
• Multiclass Classification: https://en.wikipedia.org/wiki/Multiclass_classification
• Multilayer Perceptron: https://en.wikipedia.org/wiki/Multilayer_perceptron
• Feedforward Neural Network: https://en.wikipedia.org/wiki/Feedforward_neural_network
• Recurrent Neural Network: https://en.wikipedia.org/wiki/Recurrent_neural_network
• Long Short-Term Memory: https://en.wikipedia.org/wiki/Long_short-term_memory
• Activation Function: https://en.wikipedia.org/wiki/Activation_function
• Logique et Raisonnement Mathématique: https://fr.wikipedia.org/wiki/Logique_et_raisonnement_math%C3%A9matique
• Représentation des Connaissances: https://fr.wikipedia.org/wiki/Repr%C3%A9sentation_des_connaissances

Wikipédia

• Agent Intelligent: https://fr.wikipedia.org/wiki/Agent_intelligent
• Calcul des Propositions: https://fr.wikipedia.org/wiki/Calcul_des_propositions
• Calcul des Prédicats: https://fr.wikipedia.org/wiki/Calcul_des_pr%C3%A9dicats
• Logique Modale: https://fr.wikipedia.org/wiki/Logique_modale
• Raisonnement Automatisé: https://fr.wikipedia.org/wiki/Raisonnement_automatis%C3%A9
• Connaissance: https://fr.wikipedia.org/wiki/Connaissance
• Gestion des connaissances: https://fr.wikipedia.org/wiki/Gestion_des_connaissances

Couleurs

• Color Tool - Material Design

Images

• Wikimedia Commons