Data Science for Chemists

IPL Summer School, CPE Lyon

4. Data Mining

John Samuel
CPE Lyon

Year: 2023-2024
Email: john.samuel@cpe.fr

Goals

• Understanding Patterns
• Data mining tasks
• Algorithms for data mining
• Feature Selection

Patterns in Nature

• Symmetry
• Trees, Fractals
• Spirals
• Chaos
• Waves
• Bubbles, Foam
• Tesselations
• Cracks
• Spots, stripes

Patterns by Humans

• Buildings (Symmetry) : Human-made structures with symmetrical patterns. Example: Gothic cathedrals, modern skyscrapers.
• Cities : Planned or organic agglomerations inhabited by humans. Example: Paris, New York.
• Virtual Environment (e.g., video games) : Digitally created spaces for human interaction. Example: Open worlds in video games, virtual simulations.
• Human artifacts : Objects made by humans in various fields. Example: Prehistoric tools, contemporary artworks.

Pattern creation

• Repetition
• Fractals : Self-similar mathematical structures at different scales.
  • Julia set: A fractal set defined by an iterative function f(z) = z² + c
  • Characteristics : produces complex repetitive patterns when visualized.

Synonyms

• Pattern recognition
• Knowledge discovery in databases
• Data mining
• Machine learning

Pattern Recognition: Approaches

• Supervised Learning: The model is trained on a labeled dataset where input examples are associated with desired outputs. The model learns to make predictions on new data based on these associations.
• Unsupervised Learning: The model is exposed to unlabeled data and seeks to discover patterns, structures, or intrinsic relationships within the data.
• Semi-Supervised Learning: A combination of the two above, using both labeled and unlabeled data for training.
• Reinforcement Learning: The model learns to make decisions by interacting with its environment. It receives rewards or penalties based on its actions, which guides its learning.

Formalization

• Euclidean vector:
  • An Euclidean vector is a geometric object characterized by its magnitude (length) and direction.
  • Euclidean vectors are commonly used to represent data as points in a multidimensional space, where each dimension corresponds to a feature or variable.
• Vector space:
  • A vector space is a collection of vectors that can be added together and multiplied by numbers (scalars).

Formalization

• Feature vector:
  • A feature vector is an n-dimensional vector that represents the features or attributes of an entity.
• Feature space:
  • The feature space is the vector space associated with feature vectors.
  • Each dimension of this space represents a particular feature, and vectors are used to position data in this space based on their features.

Examples of Features

• Images: In the context of images, feature vectors can be constructed from pixel values. Each pixel can be considered as a dimension, and a feature vector will contain the values of all pixels, thus representing an image as a vector.
• Texts: For texts, feature vectors are often constructed based on the frequency of words, phrases, or tokens in a document. This allows the representation of textual content using numerical values, which is essential for text analysis and information retrieval.

Formalization

• Feature construction¹:
  • Feature construction involves creating new variables or attributes from those already present in the data.
  • This step can be crucial for improving the performance of machine learning models by introducing relevant information and eliminating noise.
• Feature construction operators:
  • Construction operators are functions or mathematical operations used to create new features from existing ones.
  • Commonly used operators include equality operators (comparisons), arithmetic operators (addition, subtraction, multiplication, division), array operators (min, max, mean, median, etc.), transformation functions, etc.
1. https://en.wikipedia.org/wiki/Feature_vector

Example

• Let Year of Birth and Year of Death be two existing features.
• A new feature called age is created. age = Year of Death - Year of Birth

Feature construction is an essential step in the data preprocessing pipeline in machine learning, as it can help make data more informative for learning algorithms.

Formalization: Supervised learning

• Let N be the number of training examples
• Let X be the input feature space
• Let Y be the output feature space (of labels)
• Let {(x₁, y₁),...,(x_N, y_N)} be the N training examples, where
  • x_i is the feature vector of i^th training example.
  • y_i is its label.
• The goal of supervised learning algorithm is to find g: X → Y, where
  • g is one of the functions from the set of possible functions G (hypotheses space)
• Scoring function F denote the space of scoring functions, where
  • f: X × Y → R such that g returns the highest scoring function.

Formalization: Unsupervised learning

• Let X be the input feature space
• Let Y be the output feature space (of labels)
• The goal of unsupervised learning algorithm is to
  • find mapping X → Y

Formalization: Semi-supervised learning

• Let X be the input feature space
• Let Y be the output feature space (of labels)
• Let {(x₁, y₁),...,(x_l, y_l)} be the l be the set of labeled training examples
• Let {x_l+1,...,x_l+u} be the u be the set of unlabeled feature vectors of X.
• The goal of semi-supervised learning algorithm is to do
  • Transductive learning, i.e., find correct labels for {x_l+1,...,x_l+u}. OR
  • Inductive learning, i.e., find correct mapping X → Y

Common Tasks in Data Mining

1. Classification
2. Clustering
3. Regression

Classifiers

• Algorithmic categorization of objects : Process of assigning classes or categories to objects via algorithms. The goal is to organize data into distinct groups to facilitate analysis and decision-making.
• Class assignment : Assigning a class or category to each object (or individual).
• Types of classification:
  • Binary classification : Assignment to two classes.
  • Multi-class classification : Assignment to multiple classes simultaneously.

Applications

• Spam vs Non-spam
• Document classification
• Handwriting recognition
• Speech Recognition
• Internet Search Engines

Formal definition

• Let X be the input feature space
• Let Y be the output feature space (of labels)
• The goal of classification algorithm (or classifier) is to find {(x₁, y₁),...,(x_l, y_k)}, i.e., assigning a known label to every input feature vector, where
  • x_i ∈ X
  • y_i ∈ Y
  • |X | = l
  • |Y | = k
  • l >= k

Classifiers

Classifiers

Let

• tp: number of true postives
• fp: number of false postives
• fn: number of false negatives

Then

• Accuracy a = (tp + tn) / (tp + tn + fp + fn)
• Precision p = tp / (tp + fp)
• Recall r = tp / (tp + fn)
• Specificity r = tn / (tp + fn)
• F1-score f1 = 2 * ((p * r) / (p + r))

Confusion Matrix

Confusion Matrix

Multiclass classification

• Discovering groups and structures in the data without using known structures in the data
• Objects in a cluster are more similar to each other than the objects in the other cluster

Applications

• Social network analysis
• Image segmentation
• Recommender systems
• Grouping of shopping items

Formal definition

• Let X be the input feature space
• The goal of clustering is to find k subsets of X, in such a way that
  • C₁.. ∪ ..C_k ∪ C_outliers = X and
  • C_i ∩ C_j = ϕ, i ≠ j; 1 <i,j <k
  • C_outliers may consist of outlier instances (data anomaly)

Cluster models

• Centroid models: cluster represented by a single mean vector
• Connectivity models: distance connectivity
• Distribution models: clusters modeled using statistical distributions
• Density models: clusters as connected dense regions in the data space
• Subspace models
• Group models
• Graph-based models
• Neural models

• Finding a function which models the data
• Assigns a real-valued output to each input
• Estimating the relationships among variables
• Relationship between a dependent variable ('criterion variable') and one or more independent variables ('predictors').

Applications

• Prediction
• Forecasting
• Machine learning
• Finance

Formal definition

• A function that maps a data item to a prediction variable
• Let X be the independent variables
• Let Y be the dependent variables
• Let β be the unknown parameters (scalar or vector)
• The goal of regression model is to approximate Y with X,β, i.e.,
  • Y ≅ f(X,β)

Linear regression

• straight line: y_i = β₀ + β₁x_i + ε_i OR
• parabola: y_i = β₀ + β₁x_i + β₁x_i² +ε_i

Linear regression

• straight line: y_i = β₀ + β₁x_i + ε_i OR
• ŷ_i = β₀ + β_1i OR
• Residual: e_i = ŷ_i - y_i
• Sum of squared residuals, SSE = Σ e_i, where 1 < i < n
• The goal is to minimize SSE

1. Support Vector Machines (SVM)
2. Decision Trees
3. Ensemble Methods (Random Forest)

Introduction

• Supervised learning approach
• Binary classification algorithm
• Constructs a hyperplane ensuring the maximum separation between two classes

Hyperplane

• Hyperplane of n-dimensional space is a subspace of dimension n-1
• Examples
  • Hyperplane of a 2-dimensional space is 1-dimensional line
  • Hyperplane of a 3-dimensional space is 2-dimensional plane

• The goal of a SVM is to estimate a function f: R^N ⨉ {+1,-1}, i.e.,
  • If x₁,...,x_l ∈ R^N are the N input data points,
  • the goal is to find (x₁,y₁),...,(x_l,y_l) ∈ R^N ⨉ {+1,-1}
• Any hyperplane can be written by the equation using set of input points x
  • w.x - b = 0, where
  • w ∈ R^N, a normal vector to the plane
  • b ∈ R
• A decision function is given by f(x) = sign(w.x - b )

• If the training data are linearly separable, two hyperplanes can be selected
• They separate the two classes of data,
  so that distance between them is as large as possible.
• The hyperplanes can be given by the equations
  • w.x - b = 1
  • w.x - b = -1
• The distance between the two hyperplanes can be given by 2/||w||

Formal definition

• Region between these two hyperplanes is called margin.
• Maximum-margin hyperplane is the hyperplane
  that lies halfway between them.
• In order to prevent data points from falling into the margin, following constraints are added
  • w.x_i - b >= 1, if y_i = 1
  • w.x_i - b <= -1, if y_i = -1
• y_i(w.x_i - b) >= 1 for 1<= i <= n

Formal definition

• The goal is to minimize ||w|| subject to y_i(w.x_i - b) >= 1 for 1<= i <= n
• Solving for both w and b gives our classifier f(x) = sign(w.x - b)
• Max-margin hyperplane is completely determined by the points that lie nearest to it, called the support vectors

Data mining tasks

• Classification (Multi-class classification)
• Regression
• Anomaly detection

Applications

• Text and hypertext categorization
• Image classification
• Handwriting recognition

Decision Trees

Decision Trees

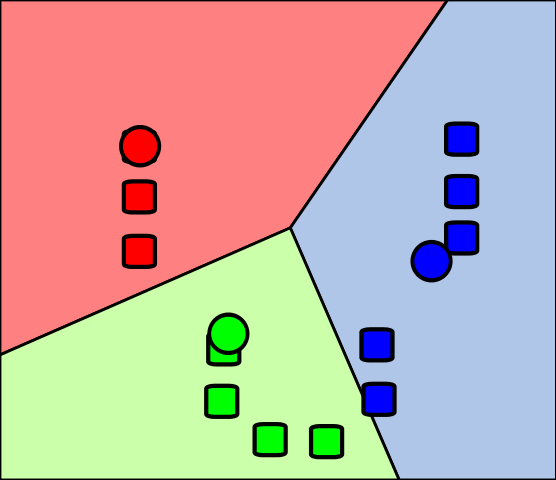
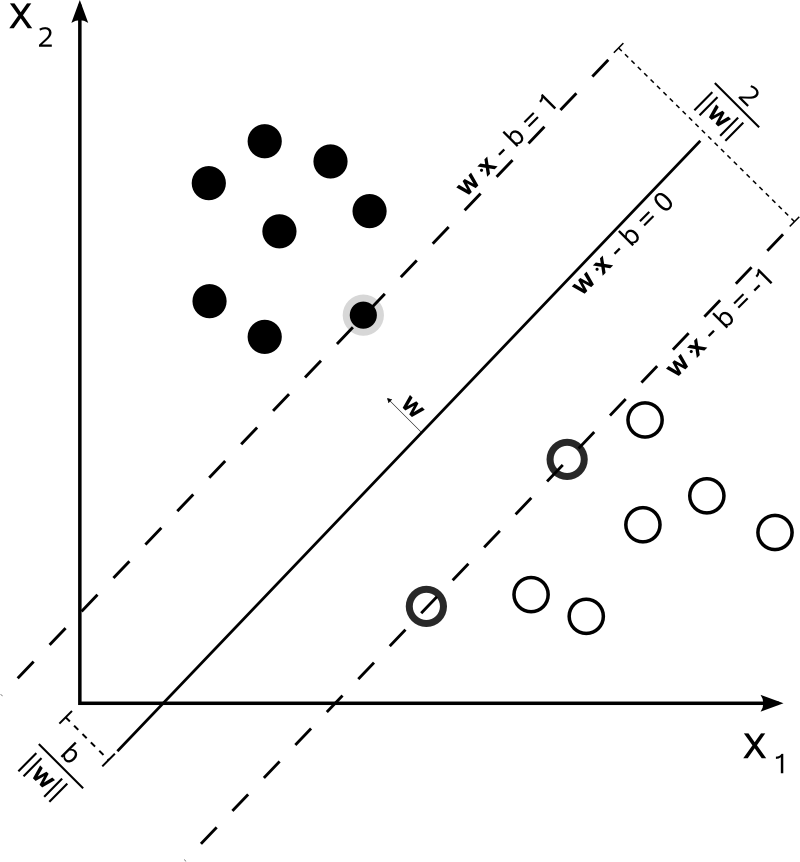
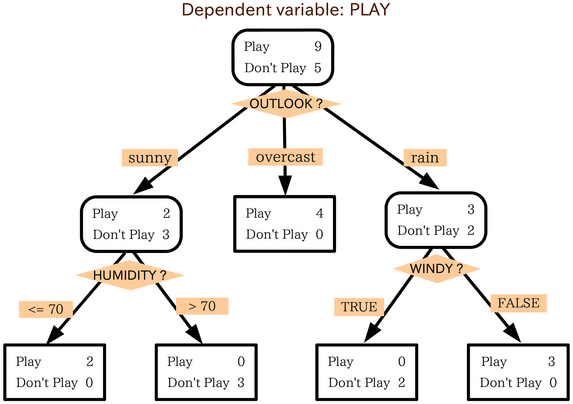
Decision trees are a powerful decision support tool that uses a tree-like model to represent decisions and their possible consequences.

• Tree model: Decision trees represent decisions in a tree structure, where each internal node represents a feature (or attribute), each branch represents a decision based on that feature, and each leaf represents an outcome or class.
• Easy to interpret: Decision trees are easy to understand and interpret, making them popular for decision-making in many fields.
• Adaptability: They can be used to model both classification and regression problems.
• Use of simple rules: Decisions are made by following simple rules based on feature values, making interpretation of results easy even for non-experts.

Applications

• Classification
• Regression
• Decision Analysis: identifying strategies to reach a goal
• Operations Research

Ensemble learning

Ensemble learning, particularly decision tree forests, is a technique that combines multiple learning models to improve predictive performance compared to a single model. Decision tree forests are obtained by constructing multiple decision trees during the training phase.

• Construction of decision trees : During the training phase, multiple decision trees are constructed using different subsets of data and/or features. Each tree is independently trained.
• Majority vote : For classification, each decision tree votes for the predicted class of a new example. The final class assigned to the example is determined by a majority vote among all the trees in the forest. For regression, the predicted values by each tree are averaged to obtain the final value.
• Stability : Decision tree forests are generally more stable than individual decision trees because they are less sensitive to variations in the training data.

• Multi-class classification : Decision tree forests are used to classify instances into one of several mutually exclusive classes. For example, classifying images into different categories such as animals, vehicles, household objects, etc.
• Multi-label classification : Unlike multi-class classification, multi-label classification allows an instance to be assigned to multiple classes simultaneously. For example, classifying documents where a document can be associated with multiple categories such as "science", "technology", "politics", etc.
• Regression : Decision tree forests can also be used for regression tasks, where the output is a continuous value rather than a discrete class. For example, predicting the price of a house based on its features.
• Anomaly detection : They can also be employed to detect anomalies or unusual behaviors in data. This can be useful in various domains such as detecting financial fraud, identifying failures in industrial systems, etc.

Feature selection is a process aimed at choosing a subset of relevant features from a large number of available features.

• This technique is widely used in fields where the number of features is high compared to the sample size, as this can lead to overfitting and high computation time.
• Feature selection is also considered a dimensionality reduction method, as it aims to reduce the number of dimensions in the feature space without losing discriminative information.
• Feature selection aims to:
  • Identify the most relevant features that contribute the most to data variability or model prediction capability.
  • Reduce the dimensionality of the feature space to improve the performance of machine learning models in terms of computation time and overfitting prevention.

Applications

• Analysis of written texts : In the analysis of written texts, feature selection is effectively used to extract the most relevant and informative elements from textual data. This can include identifying keywords, named entities, specific linguistic patterns, or other features essential for text analysis tasks such as document classification, information extraction, or summary generation. Feature selection in this context aims to reduce the dimensionality of textual data while preserving their relevance and expressiveness for subsequent analysis tasks.
• Analysis of DNA microarray data : In genomics and bioinformatics, DNA microarrays generate highly dimensional datasets that often require dimensionality reduction to identify the most significant genes or DNA sequences associated with particular phenotypes, such as diseases or biological responses.

Formal defintion[8]

• Let X be the original set of n features, i.e., |X| = n
• Let w_i be the weight assigned to feature x_i∈ X
• Binary feature selection assigns binary weights whereas continuous feature selection assigns weights preserving the order of its relevance.
• Let J(X') be an evaluation measure, defined as J: X' ⊆ X → R
• Feature selection problem may be defined in three following ways
  1. |X'| = m < n. Find X' ⊂ X such that J(X') is maximum
  2. Choose J₀, Find X' ⊆ X, such that J(X') >= J₀
  3. Find a compromise among minimizing |X'| and maximizing J(X')

Research articles

1. From data mining to knowledge discovery in databases, Usama Fayyad, Gregory Piatetsky-Shapiro, and Padhraic Smyth, AI Magazine Volume 17 Number 3 (1996)
2. Survey of Clustering Data Mining Techniques, Pavel Berkhin
3. Mining association rules between sets of items in large databases, Agrawal, Rakesh, Tomasz Imieliński, and Arun Swami. Proceedings of the 1993 ACM SIGMOD international conference on Management of data - SIGMOD 1993. p. 207.
4. Comparisons of Sequence Labeling Algorithms and Extensions, Nguyen, Nam, and Yunsong Guo. Proceedings of the 24th international conference on Machine learning. ACM, 2007.

Research articles

5. An Analysis of Active Learning Strategies for Sequence Labeling Tasks, Settles, Burr, and Mark Craven. Proceedings of the conference on empirical methods in natural language processing. Association for Computational Linguistics, 2008.
6. Anomaly detection in crowded scenes, Mahadevan; Vijay et al. Computer Vision and Pattern Recognition (CVPR), 2010 IEEE Conference on. IEEE, 2010
7. A Study of Global Inference Algorithms in Multi-Document Summarization. McDonald, Ryan. European Conference on Information Retrieval. Springer, Berlin, Heidelberg, 2007.
8. Feature selection algorithms: A survey and experimental evaluation., Molina, Luis Carlos, Lluís Belanche, and Àngela Nebot. Data Mining, 2002. ICDM 2003. Proceedings. 2002 IEEE International Conference on. IEEE, 2002.
9. Support vector machines, Hearst, Marti A., et al. IEEE Intelligent Systems and their applications 13.4 (1998): 18-28.

Online resources (English Wikipedia)

• Accuracy, Recall, Precision, F-Score & Specificity, which to optimize on?
• Patterns in Nature
• Data Mining
• Statistical classification
• Regression analysis
• Cluster analysis
• Association rule learning
• Anomaly detection

• Sequence labeling
• Automatic summarization
• Pattern recognition
• Scikit-learn

Online resources (English Wikipedia)

• Support Vector Machines
• Decision tree learning
• Stochastic gradient descent

Colors

• Color Tool - Material Design

Images

• Wikimedia Commons